Relationships Between Cognitive Styles and Indigenous Students’ Mathematics Academic Outcomes

Murni Sianturi Riska Suliantin and Hariani Fitrianti

2022 VOL. 9, No. 3

Abstract: This article explores the link between cognitive styles and Indigenous students’ mathematics academic outcomes. There were three different groups of Indigenous West Papuan students participating in this study: 9 junior high school students, 12 senior high school students, and 46 university students. Data were collected from the results of the group embedded figure test and the previous semester's scores and analysed using a quantitative approach. In contrast to previous studies, the results indicated no significant correlation between cognitive styles and mathematics academic outcomes for junior and senior high school students. However, the different cognitive styles showed a significant contribution for university students. As Indigenous students pursue a higher level of education, their cognitive styles would influence their mathematics academic outcomes.

Keywords: Indigenous students, cognitive styles, mathematics academic outcomes, mathematics learning achievement, gender.

Introduction

The contested discourses about the success of Indigenous students have continued to be discussed among researchers (Chung et al., 2021; Harrison, 2011; Lowe, 2017;  Sianturi et al., 2018). Underperformance among Indigenous students has been found globally (Abdullah et al., 2013; Burridge et al., 2012; Dhir, 2015; Chen, 2016; Jacob, 2017; Sianturi et al., 2018). For example, after several years of implementing a range of improvement strategies in Australia, the percentage attainment rates of Indigenous students in terms of literacy (Department of the Prime Minister and Cabinet, 2018; Riley & Webster, 2016) and numeracy performance lag behind those of non-Indigenous students (Department of the Prime Minister and Cabinet, 2018).

The literature also notes that the literacy and numeracy performances of Indigenous West Papuan students are lower than non-Papuan students (BPS, 2020; Sianturi et al., 2018). According to the latest report on schooling annual evaluation in 2019, junior high and senior high school students' average scores on compulsory subjects were below the national average (Kementrian Pendidikan dan Kebudayaan [Indonesian Ministry of Education and Culture] (Kemendikbud), 2019). Indigenous West Papua students in Merauke Regency have the lowest scores in mathematics out of all the subjects offered in schools (Kemendikbud, 2019). Based on a report from previous research, it was discovered that West Papuan students in higher education had only a 43 out of 100 score on the basic mathematical ability test (Sianturi & Suryani, 2017).

The mathematics academic achievement gap between Indigenous and non-Indigenous students has become a worldwide issue. The ongoing legacy of colonisation that persistently has impacts on Western mainstream education, which numerically assesses the academic success of Indigenous from colonial lenses, and the global neoliberal views that prioritise standardised scores, perpetuates placing these students in a marginalised position (Rigney et al., 2020;  Sianturi, Chiang, et al., 2022). Despite the constant educational disadvantage faced by Indigenous students, there remains a limited understanding of the source of the educational gap and of ways to improve Indigenous students' outcomes and close the gap.

Although governments and schools have attempted to increase the students' learning achievement, the attempts seem to achieve less. For example, the Indonesian government strives to enhance Papuan students' academic success, making them equivalent to their Indonesian peers, however, what the government has undertaken provides limited space for Papuan students to multiply their potential (Rahmawati, 2004; Sianturi, Chiang, et al., 2022). Why? Because these efforts are more likely to assimilate them into a community different from them (Sianturi, Chiang, et al., 2022). This community is inaccessible and culturally divisive (Yunkaporta, 2009). If the focus of the government and teachers is only on how to make the scores of Indigenous students equal to non-Indigenous students, then the divide will never be closed. Only if all parties can see the uniqueness and distinctive characteristics of Indigenous students and their needs, and set aside the intention of equating all students with a standardised value, then the conceptualisations of knowledge and learning will be more inclusive (Munroe et al., 2013; Perso, 2012). This would encourage teachers to focus on efforts to understand students and dig deeper into their potential and the way they think and learn so that teachers will be able to design lessons that are appropriate and accessible for them (Hogg & Volman, 2020; Sianturi et al., 2018).

One of students’ characteristics seen as influencing the success of students' mathematical performance that teachers might consider is cognitive style. Several studies have shown that there is a significant correlation between the classification of students' cognitive styles on their mathematics learning outcomes (Azlina et al., 2018; Jantan, 2014; Nur & Palobo, 2018). That is, the classification of certain cognitive styles of students affects them in approaching mathematics, which leads to their success in learning that subject. Considering the low performance of Indigenous West Papuan students in mathematics, our study focused on identifying the relationship between their mathematics academic outcomes, cognitive styles, and gender.

Literature Review

Cognitive Styles and Indigenous Students’ Ways of Learning

Cognitive styles refer to the terminology used to describe an individual’s unique way of receiving and processing information (Umaru, 2013; Witkin et al., 1977). Individuals may proceed with cognition differently, including attention, memory, awareness, understanding, perception, and reasoning (Macneil, 1980; Umaru, 2013). Although cognitive styles are popular in psychological disciplines, cognitive styles have become expansive in educational fields. A growing literature has shown the relevance of cognitive styles to students’ learning process (Jantan, 2014; Singer et al., 2017; Umaru, 2013), in which they are considered a determining element of students’ uniqueness in perceiving and managing information from the environment (Kozhevnikov, 2007; Singer et al., 2017).

Cognitive styles are distinct from cognitive ability, which is often measured by intelligence tests (Umaru, 2013; Witkin et al., 1977). Although cognitive style and cognitive ability probably influence learning practice performance, several cognitive styles may match some practices more than others and vice versa (Kozhevnikov, 2007; Riding & Sadler‐Smith, 1997; Singer et al., 2017; Witkin et al., 1977). Cognitive styles reflect qualitative rather than quantitative differences between individuals in their thinking processes (Riding & Sadler‐Smith, 1997; Vega-Vaca & Hederich-Martínez, 2015; Witkin et al., 1977). While cognitive ability emphasises students’ intellectual level more, cognitive style is more about students’ ways of thinking, their steady mode of intellectual and perceptual functioning (Umaru, 2013), and their attitudes toward interpreting situations and resolving matters in mind (Desmita, 2012; Umaru, 2013). The students’ preferred method of organising information leads them to develop knowledge (Witkin et al., 1977), enables combination in a cross-ability and personality, and ultimately manifests it in several activities (Desmita, 2012).  

Witkin et al. (1977) studied individuals' ways of thinking profoundly and discovered two classifications of cognitive styles: field-independent (FI) and field-dependent (FD). The characteristics of a person classified as FI are: 1) proceeding with information in part patterns and analytic ways and having a tendency to one’s own self-defined purpose; 2) feeling challenged to learn and comprehend social information and contents and, therefore, requiring certain assistance (Blanton, 2004; Witkin et al., 1977);  3) developing inductive reasoning to interpret inputs (Saville-Troike, 2012) one’s own structures in unstructured situations (Blanton, 2004; Witkin et al., 1977), and feeling efficient working alone (Vega-Vaca & Hederich-Martínez, 2015; Volkova & Rusalov, 2016); 4) not being influenced by criticism and more introverted (Vega-Vaca & Hederich-Martínez, 2015); 5) tackling problems without explicit guidance and instructions (Witkin et al., 1977). Meanwhile, characteristics of a person classified as FD are: 1) proceeding with information in a whole pattern and defined structures and having a tendency to require reinforcement; 2) showing more interest in social contents and, therefore, memorising social information well (Blanton, 2004; Witkin et al., 1977); 3) developing deductive reasoning to interpret inputs (Saville-Troike, 2012), having difficulty with structured learning material (Blanton, 2004; Witkin et al., 1977), and enjoying working in a team (Volkova & Rusalov, 2016); 4) being influenced by criticism and more extroverted (Vega-Vaca & Hederich-Martínez, 2015); 5) needing clear instruction mnemonics or metaphors to solve problems (Blanton, 2004).

Research in Indigenous education suggests recognising Indigenous children’s ways of learning (Krakouer, 2015; Yunkaporta, 2009). How Indigenous students think is distinct from non-Indigenous students. For instance, Harris (1984) asserted that Australian Aboriginal students have unique elements of learning that are the same as other non-Aboriginal students have. While non-Aboriginal pupils get used to school-based learning, Aboriginal children prefer informal learning. However, many parties, even the teachers themselves, do not understand this difference, thus generalising the learning approaches between Indigenous and non-Indigenous students (Hughes & More, 1997). Yunkaporta (2009) continued similar research and found eight Indigenous ways of learning: 1) Deconstruct/Reconstruct: scaffolding and framing, working from a whole pattern to parts; 2) Learning Maps: explicitly visualising processes; 3) Community Links: embracing local perspectives and learning from the community; 4) Symbols and Images: utilising images, metaphors, and symbols to understand concepts; 5) Non-verbal: using intra-personal and kinaesthetic skills to think, organise information, and learn; 6) Land Links: place-based learning, linking content to local land and environment; 7) Story Sharing: approaching learning through narrative; 8) Non-linear: producing innovations and understanding by thinking laterally or combining systems (pp. 46-50).

The concepts Yunkaporta (2009) discussed resonate with the FD classification criteria — there are some commonalities. Evidence corroborates that some Indigenous groups (e.g., Native American and Australian Aboriginal learners) tend to be more FD (Pewewardy, 2002; Rasmussen et al., 2004). However, it should be noted that this prevalence is not general for all Indigenous peoples; even within one group, the tendency to be FD cannot be generalised (Rasmussen et al., 2004). This is further explained by Kozhevnikov (2007), that although cognitive styles tend to be identical and stable in each individual, they are not consistent over time because changes may occur in line with responses to specific environmental situations.

Cognitive Styles and Mathematics Learning

There is a link between students’ cognitive styles and their mathematical achievement (Jantan, 2014).  This positive correlation has drawn several researchers’ interest to its profound impacts on more exceptional mathematical skills: creativity (Azlina et al., 2018; Singer et al., 2017), problem-solving (Ademola, 2015; Faradillah et al., 2018), mathematical communication (Pratiwi et al., 2013) and particular subject areas, such as geometry (Singer et al., 2017) and algebraic reasoning tasks (Chrysostomou et al., 2013; Rosita, 2018). These studies’ findings underscored the importance of delving in more substantial depth into how cognitive styles influence mathematics learning. Singer et al. (2017) considered cognitive style a good predictor of students' mathematical creativity in a comprehensive analysis. Some of these studies also provided recommendations for the idea of dynamic balance in teaching mathematics by embracing students' cognitive styles (Chrysostomou et al., 2013; Singer et al., 2017).

Cognitive Styles and Gender

The literature has recognised the relationship between gender and mathematics performance (Goodchild & Grevholm, 2009; Lin et al., 2020; Munroe, 2016). There is a higher performance rate among males in mathematics than among females. During the mathematics learning process, compared to their male peers, girls tend to exhibit a less positive attitude towards mathematics (Munroe, 2016). For questions in which they are uncertain of the answer, girls are less likely to take a risk (Goodchild & Grevholm, 2009). The discrepancy also appears in ways they approach mathematical problems. When determining the solutions process and presenting their results, boys are more likely to use diagrams, while girls prefer to utilise traditional methods and narratives (Munroe, 2016).

It is evident that there is a tendency for males to perform better on mathematics tests than females, when it comes to learning mathematics, and according to Arnup et al. (2013), these discrepancies might be partly explained by the differences in the cognitive styles of the individuals. Their study involving 190 primary school pupils aged between 8 and 11 years reported the relationship between cognitive styles, mathematics performance, and gender. Based on the results presented, there was a difference in the way boys and girls perform mathematics based on their cognitive styles. It was found that there was a significant interaction between gender and cognitive styles in the context of mathematics learning. Compared to girls with the FI classification, boys with that classification performed significantly better.
Moreover, Pathuddin et al. (2019) specifically studied the characteristics of male students with different cognitive styles in solving mathematics problems. Boys with the FI cognitive style were typically capable of reshaping and connecting new information to the knowledge they already possessed and organised in resolving problems. Contrary, it is difficult for boys with the FD classification to solve problems effectively as they feel challenged to organise their approach and connect new information to their existing knowledge.

These previous studies focused more on the relations to mathematics performance, cognitive styles, and gender among students in general. Although findings of studies that explored the prevalence of Indigenous students’ cognitive classifications were presented in the previous discussion, those studies did not examine the relationships to mathematics academic performance, cognitive styles, and gender. Therefore, a study that identifies the relationships between mathematical performance, cognitive styles, and gender among Indigenous students is considered necessary. Moreover, this is because Indigenous students have different ways of learning from students in general.

Research Objectives and Questions

This research profoundly investigated the relationships between Indigenous students’ cognitive styles, gender, and mathematics academic outcomes. This study is critical to help teachers develop teaching strategies more relevant to Indigenous students' characteristics and uniqueness and is accessible and inclusive for Indigenous students. This study adds to the literature on cognitive styles and Indigenous students' mathematical skills. The following research questions (RQs) were used to accomplish the objective of this study:

RQ1: Is there a significant association between gender and Indigenous students’ cognitive style classification?

RQ2: Is there a significant relationship between cognitive styles and mathematics academic outcomes among Indigenous West Papuan students?

Research Framework

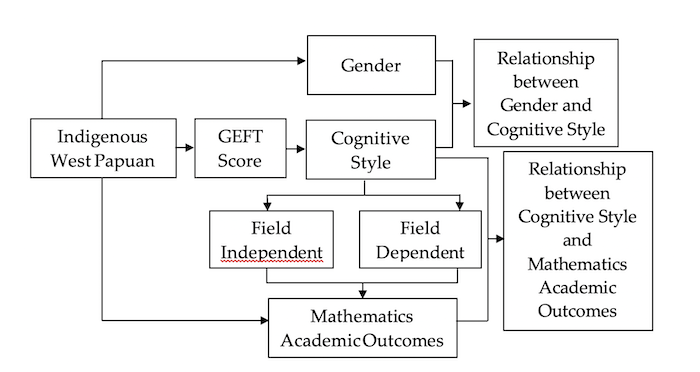
This study was structured according to the research framework illustrated in Figure 1. In the present study, the relationship between cognitive styles, genders, and mathematics academic outcomes was examined among Indigenous West Papuan students who were enrolled in this study. There are three main pieces of information required in order to identify such a relationship, including gender, cognitive style classification, and mathematics academic outcomes. This study first examined whether or not there is a relationship between gender and cognitive styles. We identified if Indigenous West Papua students' gender affects their prevalence of cognitive style. The relationship between cognitive style classification and mathematics academic outcomes was sequentially investigated. Through correlation analysis, we intended to understand if the prevalence of the cognitive style of Indigenous West Papua students affected their mathematics academic outcomes.

Figure 1: Research Framework Methods

Research Methodology

This study examined the relationship between cognitive styles, genders, and mathematics academic outcomes among Indigenous West Papuan students. In case-study research methods, researchers can explore the data closely within the context of a particular situation or issue in order to assess its relevance (Zainal, 2007). Typically, a small number of individuals, or limited geographical areas, are chosen as the subjects of a case study  (Creswell, 2014; Zainal, 2007). There is a weakness that a case study may not have a broad application, due to the fact the statistical requirements may not be met when analyzing small data sets. If that is the case, case studies could be limited in their application (Davies & Beaumont, 2011). There is no one particular tradition of social scientific research that inspired case studies. "Case study is defined by individual cases, not by the methods of inquiry used" (Stake, 1994, 236). Depending on the nature of the case, it can be complex or simple (Stake, 1994). It is also possible for case studies to be quantitative and/or qualitative. Using quantitative analysis, case studies can include both empirical and analytical elements (Mills et al., 2010).

Because our study concentrated on a small group of Indigenous West Papuan students inhabit in the Merauke area who had a specific case in terms of low mathematics performance, we considered our study a simple case study using quantitative analysis, as we discussed in the previous section regarding the low mathematics performance of Indigenous West Papuan students at different school levels. Depending on each child's age and grade level, as well as the academic area in which the child was studying, the role of cognitive style in relation to academic achievement could vary (Saracho, 1988). We were interested in identifying how the cognitive styles differ for each level. Research on cognitive styles using GEFT is generally intended for individuals or groups of young people over ten years old, particularly research that specifically discusses the area of mathematics. Therefore, in our study, we intended to examine these three different levels (i.e., junior and senior high schools, and university).

Population and Sample

Although, in order to sample cases in a quantitative study it is necessary to have some understanding of both the cases and the populations within which they are drawn, Thompson (1999) and Uprichard (2013) asserted that we need to know what kinds of methods are most appropriate to deal with certain cases. Some cases in quantitative studies employ non-probability (non-random) sampling for some consideration (Vehovar et al., 2016). As a way of optimising response rates, non-probability sampling is also introduced in quantitative research (Asiamah et al., 2022). Non-probability sampling methods are often used by researchers for practical reasons. There are specific criteria that are used to select non-probability samples, such as: practicality (data can be collected more easily and efficiently through a sample); necessity (not all populations can be studied because they are too large or inaccessible); cost-effectiveness (there is expense involved — equipment, travel, etc.) and a reduction in participant enrollment manageability (using smaller datasets, the process of storing and conducting statistical analyses is easier and more reliable) (Asiamah et al., 2022; Uprichard, 2013; Vehovar et al., 2016). This sampling method will help particularly early career epistemologists who might have to consider cost-effectiveness (since many of them might not receive funding or sponsorship), conduct feasible studies and obtain an understanding of reporting their practices plausibly (Asiamah et al., 2022). To bridge tensions between methodological and practical activities (Uprichard, 2013), researchers must determine the limits of inference (Asiamah et al., 2022) and whether or not it is intended to generalise population. As long as there is researcher awareness of the epistemological perspectives they adopt, the door is opened to a set of other discussions.

Although this study employed a quantitative approach, some practical consideration was made to select non-random sampling. As early-career researchers, cost-effectiveness, practicality, and necessity were the most reasonable justification that we took into account. Therefore, it is less likely that we could make statistically valid inferences about the population at large based on nonrandom selection methods rather than based on a probability sample.

Our study focused on a group of Indigenous West Papuan students who lived in the Merauke District and who had a specific case in terms of low mathematics performance. The number of Indigenous Papuan people is decreasing compared to non-Indigenous, and, in general, Indigenous Papuans live in remote areas, where access to them is quite difficult and costly. Therefore, we identified schools and universities that we could reach, as well as classes and majors that have a fairly large proportion of Indigenous Papuan students. We decided to select two schools and one department of a local university. For confidentiality purposes, the names of the schools and university were anonymous. After discussing with homeroom teachers at each school and the head of the Department of Primary Teacher Education, we recruited the seventh grade for the junior high school, the eleventh grade for the senior high school and the second- and third-year students for the university. All participants were Indigenous West Papuans (n = 67), in which n = 9 were junior high school, n = 12 senior high school, and n = 46 university students (Table 1).

Table 1: Demography of Participants

Tool Used

A group embedded figure test (GEFT) was given to gather information about students’ cognitive styles. GEFT is a set of psychometric tests developed by Witkin et al. (1977) and commonly used to classify individuals as FI or FD learners. GEFT takes 15 minutes to complete. It consists of three subcategories: subcategory I (a part of training, three minutes to complete), which consists of seven items; subcategories II and III (main parts, six minutes to complete for each), respectively, comprise nine items − one point for each correct answer and zero for the wrong answer. The maximum total score is 18, and the minimum is zero. If a GEFT taker gains a total score in the range of 0 to 9, he/she is classified as FD, while in the range 10-18, he/she is classified as FI (Kamaruddin et al., 2004).

The GEFT is a standardised test and has been tested across a wide range of cultures to ensure its reliability and validity. Since the GEFT was published, some scholars have tested and employed it, and it shows a strong correlation ranging from .60 to .90 (Fyle, 2009; Jantan, 2014; Lis & Powers, 1979; Panek et al., 1980; Witkin et al., 1971). This correlation remains strong even when it is translated in Indonesian (Kamaruddin et al., 2004;  Nugraha & Awalliyah, 2016; Puspananda & Suriyah, 2017) and employed in the Merauke Regency (Nur & Palobo, 2018; Nur & Nurvitasari, 2017). Puspananda and Suriyah (2017) in their research on factor analysis on the GEFT to measure cognitive styles found that the GEFT instrument has one dominant dimension, namely, cognitive styles. The validity and reliability show the internal consistency of the GEFT, and, therefore, GEFT is ready to use (Puspananda & Suriyah, 2017). This consideration led our study to use a translated version of GEFT (Kamaruddin et al., 2004;  Nur & Nurvitasari, 2017) without testing it.

Data Collection and Analysis

There were two kinds of data gathered in this study, one was the information about students' cognitive style classifications, and another was students’ mathematics learning achievements. Students’ cognitive styles were collected from the GEFT results of each student. As this study is a continuation of previous research (Sianturi, Suliantin, et. al., 2022), where the cognitive style classifications of the junior and secondary high school students in that study were used for this study. We distributed GEFT to university students (Appendix A).

Students’ mathematics academic outcomes for junior and secondary high school levels were gathered from mathematics academic scores from the latest semester. Meanwhile, the mathematics academic outcomes of university students were collected from their grades in their geometry and measurement course. All scores here use percentage grading systems with the scale of 0-100. 

We employed Fisher’s exact test value, independent t-test, and Nonparametric Correlation (Spearman Rho) assisted by SPSS Statistic 26 to analyse the data (Creswell, 2014; Creswell & Guetterman, 2019). Fisher’s exact test value was utilised to determine whether there is a significant association between gender and students’ cognitive style classification (RQ1). Meanwhile, independent t-test, and Nonparametric Correlation (Spearman Rho) were employed to identify whether there is a significant relationship between cognitive styles and mathematics academic outcomes among Indigenous West Papuan students (RQ2).

Ethical Clearance

Ethical approval was granted from the local ethics committees of the local university, the head of the department, and the principals of each school. All participants provided informed consent. The names of each school and university were kept anonymous for confidentiality purposes.

Results

Gender Preferences

As our data sample sizes were too small and data violated an assumption for Chi-Square tests, we used exact Fisher’s exact test value to discover whether the number of FI and FD learners was associated with the gender of the students. Table 2 shows that the p-value of 1.000 (for junior high school and university students) and the p-value of .333 (for senior high school students) were greater than .05. Thus, we concluded there was no significant association between gender and students’ cognitive style classifications (FI and FD).

Table 2: Cognitive Style Classifications and Gender

Cognitive Styles and Learning Achievement

Table 3 provides the relationship between GEFT results and student mathematics academic outcomes. For junior high school students, it shows p-values = .412 (p > .05) and Spearman correlation coefficient (r) = .313 and for senior high school students, p-values = .181 (p > .05) and Spearman correlation coefficient (r) = .414. Differently, for university students, p-values = .002 (p <. 01) and Spearman correlation coefficient (r) = .438.

Table 3: Correlation between Mathematics Learning Achievement and GEFT Scores

*95% confidence level

**Significance at the .01 level

Meanwhile, students’ cognitive styles did not significantly affect either junior high school or senior high school students’ learning outcomes; they significantly affected the learning outcomes of the university students. Although the cognitive styles of junior high school and senior high school students positively affected their learning outcomes, the correlation was small.

Table 4: The Effect of Cognitive Styles on Mathematics Academic Outcomes

a Levene’s test, variance is homogenous at 95% confidence level

b Levene's test is not computed because there are less than two non-empty groups.

*Significance at the .05 level

Prior to using independent t-test, we tested whether the data were normally distributed. The results of normality test for each level showed p-values = .151 (p < .05), p-values = .200 (p < .05), p-values = .000 (p < .05), which means all data distributed normally and independent t-test could be applied (Appendix B). The effect of cognitive style classifications on mathematics academic outcomes is described in Table 4. It showed that p-values =.472 (p > .05), p-values =.026 (p < .05), and p-values =.032 (p < .05), for each junior high school, senior high school, and university students, in order. The differences in FI or FD classifications only positively influenced mathematics academic outcomes of the senior high school and university students. If we compare the correlation value of junior high school, senior high school, and university students and the description in Table 4, we discover that students' cognitive styles provide greater influence as students age. Students with the FI classification were more likely to have better learning outcomes than students with the FD classification, in line with their ages. Table 5 shows that p-values = .014 (p <. 01) and Spearman correlation coefficient (r) = .369. It shows that the relationship between the FD and mathematics outcomes of university students was significantly correlated.

Table 5: Relationship between Field-Dependent and Mathematics Outcomes of University Students

**Significance at the .01 level

Discussion

In previous and recent research, it has been noted that cognitive styles have a positive connection with many cognitive attributes (Umaru, 2013; Volkova & Rusalov, 2016) and mathematics (Chrysostomou et al., 2013; Jantan, 2014; Rahman, 2013; Singer et al., 2017; Suranata et al., 2019). However, our findings support a slightly different point of view. This study’s findings revealed that Indigenous students’ cognitive styles, both junior high school and senior high school, did not significantly correlate with students' mathematics learning outcomes. Although the correlation was positive, the cognitive styles showed a small contribution to supporting Indigenous students in achieving their learning outcomes.

Meanwhile, higher education students' cognitive styles significantly influenced their learning outcomes. However, it was seen that the positive correlation became more noticeable as the students’ grade level increased. A small correlation for younger students was also discovered by Jantan (2014), where cognitive styles were more likely to influence students’ outcomes as the child matures.

This may occur because of the way teachers deliver mathematics material that is not relevant to the students’ environment. Yunkaporta (2009) argues that educators often focus on linear viewpoints, a part of Western-oriented pedagogy, within school practices, which further marginalises Indigenous students by preventing them from reconstructing their own knowledge. The learning outcomes collected in this study were analysed together with GEFT scores that were mathematics academic outcomes measured according to standard scores. Given the small contribution of cognitive styles to mathematics academic outcomes for younger students, this may be acceptable. A study involving Papuan students aged 10-12 years by Sianturi et al. (2018) also found that the delivery of learning materials for Papuan students was often monopolised by the dominant culture, making it difficult for students to grasp mathematics learning. Furthermore, another study stated that the education implemented in many schools in West Papua attempted to alienate Papuan students from their environment and culture (Sianturi, Chiang, et al., 2022).

However, it should be noted that this needs to be studied with a qualitative approach. The aim is to see how Indigenous students' ways of learning, culture, the environment, and even their gender, affects Indigenous Papuans' cognitive styles prevalence and the ways students capture information conveyed during the mathematics learning process. Previous studies that discovered a positive correlation between cognitive styles and mathematical achievement involved students in general (e.g., Ademola, 2015; Azlina et al., 2018; Chrysostomou et al., 2013; Faradillah et al., 2018; Pratiwi et al., 2013; Rosita, 2018; Singer et al., 2017). Thus, more similar studies involving Indigenous students’ mathematics learning are required. Topics about the relevance of Indigenous ways of learning and cognitive styles to students' mathematical abilities, but not taken from standardised mathematics outcomes, might be worth considering for further research.

Other than the insignificant differences between cognitive style and learning outcomes against previous studies' results (Scholar & Abdurauf, 2015) , our results also identified slight differences according to gender. Our research results indicated no significant association between Indigenous students' gender and cognitive style classification. In other words, no matter whether an Indigenous West Papuan student was a boy or a girl, his or her cognitive style would not be affected. However, we could not articulate this statement strongly because of the limited number of participants we studied.

Conclusion and Recommendations

This study sought the relationship between cognitive styles and mathematics academic outcomes among Indigenous West Papuan students. There is no significant correlation between the Indigenous students’ cognitive styles and mathematics academic outcomes at the junior and senior high school level. Indigenous students with different cognitive styles might show a small improvement in accomplishing their learning outcomes. As Indigenous students pursue a higher level of education, their cognitive styles will influence their mathematics academic outcomes.

The findings of this study provide recommendations for school practices and policymakers. Teachers should recognise Indigenous students' cognitive styles when developing teaching instructions and assessments. Knowing Indigenous students’ diverse characteristics and needs might help teachers create more culturally appropriate lessons for students. As cognitive styles might influence students’ mathematics academic outcomes as their school level increase, teachers might consider their cognitive classifications for each school level.

The results of the study should be viewed within the context of several limitations. Considering the small number of participants and the fact that we employed non-probability sampling in this study, it is not possible to generalise the results of this study. Thus, a similar procedure with a larger sample size could be applied for future research with probability sampling. Studies using qualitative approaches to find the relationship among Indigenous students' ways of learning, cognitive styles, gender, culturally responsive approaches, and their impacts on mathematical performance might be considered for future research.

Acknowledgements: We are thankful for all students who dedicated their time and energy to take part in this research. We also express our gratitude to the homeroom teachers and principals of the junior and senior high schools, and the head of the Department of Primary Teacher education who supported and facilitated this research. The meaningful input and feedback from two anonymous peer-reviewers and colleagues that improved this article is also highly appreciated.

Funding: There was no financial support received by the authors from any organisation for the work submitted for publication.

Disclosure Statement: The authors reported no potential conflict of interest.

References

Abdullah, R. Bin, Mamat, W. H. W., Amir Zal, W. A., & Ibrahim, A. M. Bin. (2013). Teaching and learning problems of the Orang Asli Education: Students’ perspective. Asian Social Science. https://doi.org/10.5539/ass.v9n12p118

Ademola, K. (2015). Predicting academic success of junior secondary school students in Mathematics through cognitive style and problem solving technique. Journal of Education and Practice, 6(4), 72-79.

Arnup, J. L., Murrihy, C., Roodenburg, J., & McLean, L. A. (2013). Cognitive style and gender differences in children’s mathematics achievement. Educational Studies, 39(3), 355–368. https://doi.org/10.1080/03055698.2013.767184

Asiamah, N., Mensah, H. K., & Oteng-Abayie, E. F. (2022). Non-probabilistic sampling in quantitative clinical research: A typology and highlights for students and early career researchers. International Journal of Applied Research on Public Health Management, 7(1), 1–18. https://doi.org/10.4018/IJARPHM.290379

Azlina, N., Amin, S. M., & Lukito, A. (2018). Creativity of field-dependent and field-independent students in posing mathematical problems. Journal of Physics: Conference Series, 947(1), 1-6. https://doi.org/10.1088/1742-6596/947/1/012031

Blanton, E. L. (2004). The influence of students’ cognitive style on a standardized reading test administered in three different formats. The University of Central Florida Orlando.

Burridge, N., Whalan, F., & Vaughan, K. (2012). Indigenous education: A learning journey for teachers, schools and communities. In Indigenous Education: A Learning Journey for Teachers, Schools and Communities. https://doi.org/10.1007/978-94-6091-888-9

Chen, S. (2016). Dawning of hope: Practice of and reflections on indigenous teacher education in Taiwan. Policy Futures in Education, 14(7), 943-955. https://doi.org/10.1177/1478210316656312

Chrysostomou, M., Pitta-pantazi, D., Tsingi, C., Cleanthous, E., & Christou, C. (2013). Examining number sense and algebraic reasoning through cognitive styles. Educational Studies in Mathematics, 83, 205-223. https://doi.org/10.1007/s10649-012-9448-0

Chung, C., Huan, H., Tseng, K., Jung, R., & Chen, C. (2021). Transformation from traditional schools to alternative schools: Curriculum leadership of the principals of Taiwanese aborigines. Asia Pacific Education Review, 22(1), 53-66. https://doi.org/10.1007/s12564-020-09663-9

Creswell, J. W. (2014). Research design: Qualitative, quantitative, and mixed methods approaches (4th ed.). SAGE Publications, Ltd.

Creswell, J. W., & Guetterman, T. C. (2019). Educational research: Planning, conducting, and evaluating quantitative and qualitative research (6th ed.). Pearson.

Davies, M., & Beaumont, T. J. (2011). Case studies: Research methods. In Study Skills for International Postgraduates (pp. 1-7). The University of Melbourne. https://doi.org/10.1007/978-0-230-34553-9

Department of the Prime Minister and Cabinet. (2018). Closing the gap: Prime Minister’s Report 2018. https://www.pmc.gov.au/sites/default/files/reports/closing-the-gap-2018/employment.html

Desmita, O. (2012). Psikologi Perkembangan Peserta Didik [Developmental Psychology of Students]. PT. Rosdakarya.

Dhir, R. K. (2015). Indigenous peoples in the world of work in Asia and the Pacific. International Labour Organization. www.ilo.org/publns

Faradillah, A., Hadi, W., & Tsurayya, A. (2018). Pre-service mathematics teachers ’ reasoning ability in solving mathematical non-routine problem according to cognitive style. Journal of Physics: Conference Series, 948(1), 1–6.

Fyle, C. O. (2009). The effects of Field Dependent/Independent style awareness on learning strategies and outcomes in an instructional hypermedia module. Florida State University.

Goodchild, S., & Grevholm, B. (2009). An exploratory study of mathematics test results: What is the gender effect? International Journal of Science and Mathematics Education, 7, 161-182. https://doi.org/10.1007/s10763-007-9114-7

Harris, S. (1984). Aboriginal learning styles and formal schooling. The Aboriginal Child at School, 12(4), 3–23.

Harrison, N. (2011). Teaching and learning in Aboriginal education (2nd ed.). Oxford University Press.

Hogg, L., & Volman, M. (2020). A synthesis of funds of identity research: Purposes, tools , pedagogical approaches, and outcomes. Review of Educational Research, 90(6), 862–895. https://doi.org/10.3102/0034654320964205

Hughes, P., & More, A. J. (1997). Aboriginal ways of learning learning styles. Annual Conference of the Australian Association for Research in Education, 1-21.

Jacob, M. M. (2017). Indigenous studies speaks to American sociology: The need for individual and social transformations of Indigenous education in the USA. Social Sciences, 7(1), 1–10. https://doi.org/10.3390/socsci7010001

Jantan, R. B. (2014). Relationship between students’ cognitive style (Field-Dependent and Field-Independent cognitive styles) with their mathematic achievement in primary school. International Journal of Humanities Social Sciences and Education (IJHSSE), 1(10), 88–93. www.arcjournals.org

Kamaruddin, M. I. Bin, Bakar, Z. B. A., Surif, J. Bin, & Li, W. S. S. (2004). Relationship between cognitive styles, levels of cognitive thinking and chemistry achievement among form four science students. Universiti Teknologi Malaysia.

Kemendikbud. (2019). Laporan Hasil Ujian Nasional  — Papua [National Examination Results Report - Papua]. https://bit.ly/3fbZsYr

Kozhevnikov, M. (2007). Styles in the context of modern psychology: Toward an integrated framework of cognitive style. Psychological Bulletin, 133(3), 464–-481.

Krakouer, J. (2015). Literature review relating to the current context and discourse on Indigenous cultural awareness in the teaching space: Critical pedagogies and improving Indigenous learning outcomes through cultural responsiveness. Australian Council for Educational Research, November, 1–21. https://research.acer.edu.au/indigenous_education/43/

Lin, A. Y., Wu, C., Chen, Z., Ku, P., Lin, Y., Wu, C., Chen, Z., & Ku, P. (2020). How gender pairings affect collaborative problem solving in social-learning context. International Forum of Educational Technology & Society, 23(4), 30-44. https://www.jstor.org/stable/26981742

Lis, D. J., & Powers, J. E. (1979). Reliability and validity of the Group Embedded Figures Test for a grade school sample. Perceptual and Motor Skills, 48, 660–662. https://doi.org/10.2466/pms.1979.48.2.660

Lowe, K. (2017). Walanbaa warramildanha: The impact of authentic Aboriginal community and school engagement on teachers’ professional knowledge. Australian Educational Researcher, 44(1), 35–54. https://doi.org/10.1007/s13384-017-0229-8

Macneil, R. D. (1980). The relationship of cognitive style and instructional style to the learning performance of undergraduate students. Journal of Educational Research, 73(6), 354-359. https://doi.org/10.1080/00220671.1980.10885265

Mills, A. J., Durepos, G., & Wiebe, E. (2010). Quantitative analysis in case study. In Encyclopedia of Case Study Research (pp. 761-764). SAGE Publications, Inc. https://doi.org/10.4135/9781412957397.n279

Munroe, E. A., Borden, L. L., Murray Orr, A., Toney, D., & Meader, J. (2013). Decolonizing Aboriginal education in the 21st century. McGill Journal of Education, 48(2), 317–337. https://doi.org/10.7202/1020974ar

Munroe, K. L. (2016). Impact of open approach on students’ understanding of mathematical concepts: A gender comparison. Graduate School for International Development and Cooperation, 22(2), 85–96. https://www.semanticscholar.org/paper/Impact-of-Open-Approach-on-Students’-Understanding-Munroe/a8fcb07b59eb2f7be012929c2d6ed346ff616dbc

Nugraha, M. G., & Awalliyah, S. (2016). Analisis gaya kognitif field dependent dan field independent terhadap penguasaan konsep fisika siswa kelas VII [Field dependent and field independent cognitive style analysis on the mastery of physics concepts for class VII students]. Prosiding Seminar Nasional Fisika (E-Journal) SNF2016, V(Oktober), 71–76. https://doi.org/10.21009/0305010312

Nur, A. S., & Nurvitasari, E. (2017). Geometry skill analysis in problem solving reviewed from the difference of cognitive style students junior high school. Journal of Educational Science and Technology, 3(3), 205–210. https://doi.org/10.26858/est.v3i3.4130

Nur, Andi Saparudin, & Palobo, M. (2018). Profil kemampuan pemecahan masalah matematika siswa ditinjau dari perbedaan gaya kognitif dan gender [Profile of students' mathematical problem solving abilities in terms of differences in cognitive style and gender]. Kreano, Jurnal Matematika Kreatif-Inovatif, 9(2), 139-148. http://journal.unnes.ac.id/nju/index.php/kreano%0AProfil

Panek, P. E., Funk, L. G., & Nelson, P. K. (1980). Reliability and validity of the Group Embedded Figures Test across the life span. Perceptual and Motor Skills, 50, 117 1-1 174. https://doi.org/10.2466/pms.1980.50.3c.1171

Pathuddin, Budayasa, I. K., & Lukito, A. (2019). Metacognitive activity of male students: Difference field independent-dependent cognitive style. Journal of Physics: Conference Series, 1218(1), 1-10. https://doi.org/10.1088/1742-6596/1218/1/012025

Perso, T. F. (2012). Cultural responsiveness and school education with particular focus on Australia’s first peoples: A review & synthesis of the literature. Menzies School of Health Research, Centre for Child Development and Education, Darwin Northern Territory.

Pewewardy, C. (2002). Learning styles of American Indian/Alaska Native students: A review of the literature and implications for practice. Journal of American Indian Education, 41(3), 22–56. https://www.jstor.org/stable/24398583

Pratiwi, D. D., Sujadi, I., & Pangadi. (2013). Kemampuan komunikasi matematis dalam pemecahan masalah matematika sesuai dengan gaya kognitif pada siswa kelas IX SMP Negeri 1 Surakarta tahun pelajaran 2012/2013 [Mathematical communication skills in solving math problems in accordance with the students’ cognitive styles at year 9 SMP Negeri 1 Surakarta academic year 2012/2013]. Jurnal Pembelajaran Matematika, 1(5), 525–538. https://jurnal.fkip.uns.ac.id/index.php/s2math/article/view/3525/2459

Puspananda, D. R., & Suriyah, P. (2017). Analisis faktor pada group embbeded figures test untuk mengukur gaya kognitif [Factor analysis on group embedded figures test to measure cognitive styles]. Seminar Matematika Dan Pendidikan Matematika UNY 2017, 225–230. http://repository.ikippgribojonegoro.ac.id/id/eprint/1384%0A

Rahman, A. (2013). Pengajuan masalah matematika ditinjau dari gaya kognitif dan kategori informasi [The submission of mathematical problems in terms of cognitive style and information categories]. Jurnal Ilmu Pendidikan, 19(1), 244–251. https://doi.org/10.17977/JIP.V19I2.4220

Rahmawati, A. (2004). Papuan ethno-political conflict: causes, contexts , and policy implication. Naval Postgraduate School.

Rasmussen, C., Sherman, J., & Baydala, L. (2004). Learning patterns and education of Aboriginal children: A review of the literature. The Canadian Journal of Native Studies, 24(2), 317-342. http://www3.brandonu.ca/cjns/24.2/cjnsv24no2_pg317-342.pdf

Riding, R. J., & Sadler‐Smith, E. (1997). Cognitive style and learning strategies: Some implications for training design. International Journal of Training and Development, 1(3), 199–208. https://doi.org/10.1111/1468-2419.00020

Rigney, L., Garrett, R., Curry, M., & Macgill, B. (2020). Culturally responsive pedagogy and mathematics through creative and body- based learning: Urban Aboriginal schooling. https://doi.org/10.1177/0013124519896861

Riley, T., & Webster, A. (2016). Principals as Literacy Leaders with Indigenous Communities (PALLIC) building relationships: One school’s quest to raise Indigenous learners’ literacy. Teaching Education, 27(2), 136-155. https://doi.org/10.1080/10476210.2015.1049261

Rosita, N. T. (2018). Analysis of algebraic reasoning ability of cognitive style perspectives on field-dependent field-independent and gender. Journal of Physics: Conference Series, 983(1). https://doi.org/10.1088/1742-6596/983/1/012153

Saracho, O. N. (1988). Cognitive Styles and Young Children’s Learning. Early Child Development and Care, 30(1-4), 213–220. https://doi.org/10.1080/0300443880300118
Saville-Troike, M. (2012). Introducing second language acquisition. Cambridge University Press.

Scholar, T. M., & Abdurauf, R. A. (2015). Cognitive styles Field Dependence / Independence and scientific achievement of male and female students of Zamfara State College of Education Maru, Nigeria. Journal of Education and Practice, 6(10), 58–64. https://files.eric.ed.gov/fulltext/EJ1081653.pdf

Sianturi, M., Chiang, C. L., & Hurit, A. A. (2018). Impact of a place-based education curriculum on Indigenous teacher and students. International Journal of Instruction, 11(1), 311–328. https://doi.org/10.12973/iji.2018.11122a

Sianturi, M., Chiang, C. L., & Sumarsono, A. (2022). The preservation of the identity and culture of the Indigenous Lanninese people of West Papua, Indonesia, through education (Preservación de la identidad y la cultura del pueblo Lani, comunidad indígena de la provincia Indonesia de Papúa Occidental, a través de la educación). Culture and Education, 34(2), 424–465. https://doi.org/10.1080/11356405.2022.2034287

Sianturi, M., & Suryani, D. R. (2017). Performansi matematika dasar siswa Papua calon guru sekolah dasar [The basic mathematical performance of Indigenous students in higher education]. In M. Palobo, A. K. Hidayat, O. Dadi, & N. R. Marwa (Eds.), Inovasi Pendidikan dan Pembelajaran dalam Rangka Percepatan Pembangunan di Daerah Pinggiran [Educational and Learning Innovation in the Context of Accelerating Development in Outlying Areas] (pp. 178–190). FKIP Musamus University.

Sianturi, M., Suliantin, R., & Sianturi, I. A. J. (2022). Culturally relevant teaching: A case study on Indigenous students’ cognitive styles and difficulties in processing information. [Manuscript submitted for publication].

Singer, F. M., Vouca, C., & Pelczer, I. (2017). Cognitive styles in posing geometry problems: Implications for assessment of mathematical creativity. ZDM, 49(1), 37–52. https://doi.org/10.1007/s11858-016-0820-x

Stake, R. E. (1994). Case studies. In N. K. Denzin & Y. S. Lincoln (Eds.), Handbook of Qualitative Research (pp. 236-247). Sage Publications.

Suranata, K., Rangka, I. B., Ifdil, I., Ardi, Z., Dharsana, I. K., Suarni, N. K., & Gading, I. K. (2019). Exploring of mathematics learning difficulties for students based on heterogeneous group and cognitive style in elementary school. Journal of Physics: Conference Series, 1157, 1–6. https://doi.org/10.1088/1742-6596/1157/3/032091

Thompson, C. (1999). If you could just provide me with a sample: Examining sampling in qualitative and quantitative research papers. Evidence-Based Nursing, 2(3), 68–70.

Umaru, Y. (2013). Influence of reflective and impulsive cognitive styles on students' achievement in mathematics among senior secondary school students. Ife PsychologIA, 21(2), 123–128.

Uprichard, E. (2013). Sampling: Bridging probability and non-probability designs. International Journal of Social Research Methodology, 16(1), 1-11. https://doi.org/10.1080/13645579.2011.633391

Vega-Vaca, M. L., & Hederich-Martínez, C. (2015). The impact of a cooperative learning program on the academic achievement in mathematics and language in fourth grade students and its relation to cognitive style. New Approaches in Educational Research, 4(2), 84–90. https://doi.org/10.7821/naer.2015.7.124

Vehovar, V., Toepoel, V., & Steinmetz, S. (2016). Non-probability sampling. In C. Wolf, D. Joye, T. W. Smith, & Y. Fu (Eds.), The SAGE Handbook of Survey Methodology (pp. 329–345). SAGE.

Volkova, E. V., & Rusalov, V. M. (2016). Cognitive styles and personality. Personality and Individual Differences, 99, 266-271. https://doi.org/10.1016/j.paid.2016.04.097

Witkin, H. A., Moore, C. A., Goodenough, D. R., & Cox, P.  (1977). Field dependent and field-independent cognitive styles and their education implications. Review of Educational Research, 47(1), 1-64. https://doi.org/10.3102/00346543047001001

Witkin, H., Oltman, P. K., & Raskin, E. (1971). Manual Embedded Figures Test, Children Embedded Figures Test, Grup Embedded Figures Test. Consulting Psychology Press, Inc.

Yunkaporta, T. K. (2009). Aboriginal pedagogies at the cultural interface [James Cook University]. http://eprints.jcu.edu.au/10974/%0A

Zainal, Z. (2007). Case study as a research method. Jurnal Kemanusiaan, 9(June), 1-6. https://core.ac.uk/download/pdf/11784113.pdf

Authors:

Murni Sianturi is an Indigenous researcher with 7 years’ experience working with Indigenous communities. She is currently a Scientia PhD Candidate at the University of New South Wales. She has more intentionally focused on issues influencing Indigenous West Papuan students, with a specific interest in mathematics learning, identity, and culture. Specifically, building on her experiences as a mathematics teacher at all school levels and a local university lecturer, her work is concerned with schooling practices and Indigenous students’ identities, impacting their experiences, culture, identities, and learning achievements. Her current research project focuses on using technology to facilitate partnerships between schools and Indigenous West Papuan parents. (http://orcid.org/0000-0002-2898-7084). Email: m.sianturi@unsw.edu.au

Riska Sulantin is a mathematics teacher at Muhammadiah Junior High School, Merauke, Papua. Born and raised in the remote area of West Papua, Riska has an interest in educating children living in rural areas. In addition to her career as a teacher, she is also actively involved in community activities. Email: rsuliantin@gmail.com

Hariani Fitrianti is a lecturer at Musamus University, Papua. Her research interests aim to explore students’ mathematical learning and statistical analysis in educational research. Email: harianifitrianti@unmus.ac.id