Viseu

Geometry is one of the great mathematical themes and traditionally integrates school programmes in most countries around the world (Arcavi, 2003). Despite the difficulties associated with its teaching and learning (Gagatsis & Geitona, 2021; Sutiarso et al., 2018), geometry has a significant historical presence and is often associated with the development of mathematics itself. This is a very rich area of knowledge, not only for its great variety and diversity, but also for the practical applications it has, for example, in computer-aided design (CAD) and geometric modeling (including design, modification and the manufacture of cars and airplanes, in the construction of buildings, etc.), robotics, medicine (in the area of medical imaging, which led to substantial new results in fields such as geometric tomography), computer animation, visual presentations and virtual reality. It is also an area that has shown considerable development (Hansen et al., 1998). Several contemporary developments in mathematics are predominantly geometric, such as work on dynamical systems (a discipline closely intertwined with the main areas of mathematics), mathematical visualisation (the art of transforming the symbolic into geometry) and geometric algebra (a representational and computational system for geometry that is entirely distinct from algebraic geometry) (Jones, 2000). And Septia et al. (2018) emphasise the role of school in the promotion of geometry learning. Deciding on the goals for school geometric training involves considering both the nature of geometry and the variety of its applications. The report promoted by The Royal Society/Joint Mathematical Council (2001, p. xii) points to the following objectives for the teaching of Geometry: “a) to develop spatial awareness, geometrical intuition and the ability to visualise; b) to provide a breadth of geometrical experiences in 2- and 3-dimensions; c) to develop knowledge and understanding of and the ability to use geometrical properties and theorems; d) to encourage the development and use of conjecture, deductive reasoning and proof; e) to develop skills of applying geometry through problem solving and modelling in real world contexts; f) to develop useful Information and Communication Technology (ICT) skills in specifically geometrical contexts; g) to engender a positive attitude to mathematics; and h) to develop an awareness of the historical and cultural heritage of geometry in society, and of the contemporary applications of geometry”.

Traditionally, the teaching of geometry is based on paper and pencil, often supported by some resources (such as the ruler or the compass), but nowadays technology offers other alternatives, as is the case of dynamic geometry environments (DGE). Their potential is such that some authors, such as Kokol-Voljc (2007), consider them to be the most suitable resource for teaching geometry. Duval (1998) even states that the use of DGE is superior to paper and pencil methods, as it allows for a dissociation between the figure and the method used in its elaboration, which promotes a focus on its properties. However, Osório, Pino-Fan and González (2017) alert us to the need to think carefully about DGE integration as this is not trivial. Several authors (e.g., Kokol-Voljc, 2007; Koyuncu et al., 2015) consider that despite the advantages offered by DGE, they should not completely replace the paper and pencil approaches, as both approaches bring important contributions to learning and conceptual understanding. Some studies, such as those conducted by Koyuncu et al. (2015) and, more recently, by Komatsu and Jones (2020), seek to consider the contributions of approaches using DGE and paper and pencil. However, as highlighted by Maschietto and Soury-Lavergne (2013) and Komatsu and Jones (2020), this is an area where further investigation is needed. And this need is particularly evident at the level of secondary education, since the few existing studies, such as those by Maschietto and Soury-Lavergne (2013), Voltolini (2018) and Faggiano, Montone and Mariotti (2018), focus on students from lower levels (primary education).

Regarding 3D Geometry, existing research considers that there is a distinction between types of reasoning in spatial ability and 3D geometric thinking (Pittalis & Christou, 2010). Spatial ability is seen as the capacity that individuals have to perform tasks including not only knowledge but also skills, such as the representation of 3D objects by 2D figures, the identification of solids and their elements, the calculation of the surface and volume of solids, or the comparation of the properties of 3D shapes (NCTM, 2007). Geometrical thinking in 3D is closely related to the domain of geometry, while the structure of spatial capabilities is closely related to cognitive development. According to Pittalis and Christou (2010), it is necessary to develop spatial capabilities to achieve the fullness of geometric thinking in 3D. Lohman (1998) considers the existence of three main factors of spatial capacity: spatial visualisation, spatial orientation, and spatial relationships. Spatial visualisation requires a student to imagine the folding and unfolding of a piece of paper that, when folded, has been perforated one or more times. Spatial orientation is the ability that students reveal in changing orientations to which a spatial configuration can be subjected. Spatial relationships are defined as the ability to mentally rotate a spatial object quickly and correctly.

For Pittalis and Christou (2010), there are four types of reasoning involved in 3D geometry thinking: (i) representation of 3D objects; (ii) spatial structuring; (iii) measurement; and (iv) conceptualisation of mathematical properties. Representation of 3D objects is a usual task in geometry, namely when drawing a 3D object, when using an orthogonal view to construct a 3D object, or even when moving from one representation to another. Spatial structuring includes the ability to perform various tasks, such as to identify the component parts of a structure, combine them and establish interrelationships between them. Measurement is related to the ability to perform various measurement tasks, such as estimating the surface area or the volume of 3D objects. The conceptualisation of mathematical properties is the ability to recognise the properties of 3D objects, such as the ability to identify solids in the real world or from 2D representations, to perceive structural elements and properties of 3D objects, to compare their structural elements (the number of vertices, faces and edges) and to compare different objects, recognising their properties and identifying relations.

There are three underlying fundamental cognitive processes that mediate the four types of reasoning described: identification of geometric properties in 3D objects; exploitation of the knowledge of the manipulation properties of 3D objects; and editing the conventions used in representing 3D objects. These cognitive processes differentiate between 3D geometry thinking and spatial abilities. The direct effects of spatial abilities on types of reasoning in 3D geometry suggest that teaching 3D geometry should integrate activities that develop spatial skills.

In this study we seek to discuss the contributions that digital technology and paper and pencil approaches can bring to 3D geometry learning. We seek to identify the differences between the two approaches, specifically: (1) What factors become relevant in one and in the other approach? (2) What does one approach facilitate over the other?

Methods

This study was based in an experience of teaching Analytical Geometry in Space, during eight lessons, challenging students to explore 18 tasks. The students started by solving the tasks using paper and pencil and later using GeoGebra. The class where the teaching experience took place was composed of 27 students (12 girls and 15 boys, age 15-16). Seven of the students assumed some difficulties in mathematics and 11 students referred to mathematics as their favorite subject (based on a school questionnaire). This was the first contact of the students with GeoGebra. The students had previously studied topics of geometry in the plane (2D) and were starting to address some of these topics in a 3D context, generalising and amplifying their previous learning. However, they had some experience at basic school with very general characteristics of the cube as a solid.

Given the nature of the goal outlined, this study presents characteristics of a quantitative and a qualitative approach in analysing the 'actions' that students performed, in pairs, in their learning activities (Bogdan & Biklen, 1994). The quantitative approach focused essentially on the characteristics of the students’ answers in what concerns their level of correctness. The qualitative approach focused also on the students’ answers but intended to analyse the reasons beyond those. For this purpose, data were collected through: (i) written records produced by the students while solving the tasks; and (ii) registrations of GeoGebra use, which were sent via email by the students. Data analysis was based on the students’ responses to the tasks. These responses were classified according to the mathematical rigor in correct answers (C), partially correct answers (PC), incorrect answers (I), and no answer (NA). The data were then organised on frequency tables. Using a qualitative approach, the students’ answers were then analysed based on the fundamental cognitive processes that mediate three of the four types of reasoning described by Pittalis and Christou (2010) and already presented: identification of geometric properties in 3D objects; exploitation of the knowledge of the manipulation properties of 3D objects; and editing the conventions used in representing 3D objects (measurement—the fourth type of reasoning—is not addressed by the set of tasks used here and is not considered in this work). On this analysis the two approaches (with paper and pencil and with digital technology) where compared.

To illustrate the activities carried out in the teaching experience, this article focuses on the study of the 'relative position of lines and planes' through the analysis of two of the tasks proposed.

Result and Discussion

In the study of the topic 'relative position of lines and planes', students began by solving the following task:

Initially, the students solved the task with paper and pencil, having as reference the different ways to define a plane and the elements of a cube, and later performed the task using GeoGebra. Table 1 summarises the analysis of students’ resolutions.

Criteria	Paper and Pencil				GeoGebra
Criteria	C	PC	I	NA	C	PC	I	NA
Representation of a cube	26	–	1	–	23	–	2	2
Plan containing two strictly parallel facial diagonals	25	2	–	–	11	–	4	12
Plane perpendicular to the plane containing two strictly parallel facial diagonals, which contains two facial diagonals	13	11	2	1	11	–	2	14
Plane strictly parallel to one of the cube faces, containing another cube face	13	5	–	9	21	–	–	6

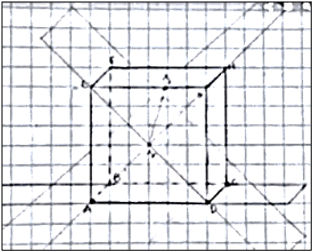
Almost all the students made the representation of the cube either with paper and pencil and with GeoGebra, meaning the cube is established in its geometrical thinking by the shape and the elements that make it up, which translates into the ability to represent in 2D an image of the 3D object. Most students revealed the ability to visualise and analyse the characteristics of this solid. Still, not all answers were correct. A25 student's answer reveals a lack of critical analysis of the representation made (Figure 1). After sketching the cube, the student did not analyse its elements to realise that he drew it with different faces (regarding the shape and dimensions of the edges), which indicates that he did not attend to the geometric properties when building the cube. Although the request was for a sketch, visually this representation may not be seen as a representation of a cube, but as that of a parallelepiped.

As for the representation of planes in the cube with paper and pencil, regarding the drawing of the plane that contains two strictly parallel facial diagonals, only two students (7%) did not do it correctly. A25 student drew a plane that clearly contains a facial diagonal but does not guarantee that it contains one that is strictly parallel to it, which is why the resolution was considered only partially correct (Figure 1). It is not clear that the plan he drew contains diagonals in parallel faces. This refers to the difficulty in mentally 'manipulating' the construction made to guarantee the condition presented.

In the representation of the plane perpendicular to the plane that contains two strictly parallel facial diagonals and that contains two facial diagonals, most students did not answer correctly (52%). A significant number of students presented an answer that was considered partially correct (41%) for not making evident the two diagonals or the plan that contains them, as illustrated in the following sketch, prepared by A2 student (Figure 2). The absence of such elements in the construction is due to the perspective considered, which does not allow us to see if the student visualised the expected perpendicular plane. This did not happen in the representation by A20 student (Figure 3).

This is a situation in which the representation chosen for the cube, and the impossibility of rotating the figure when using paper and pencil, prevents us from representing the plane as a parallelogram, as defined in the 2D representation agreed for a plane. By the representation, it is not possible to guarantee that the student has mentally visualised the plan in question, but it is also not possible to guarantee that he did not. This is an interesting situation due to the difference with a situation using technology. In this last case, it would be possible to rotate the figure and visualise the plan.

As for the two representations considered incorrect, regarding the item under analysis, they present at least one plane that does not contain one of the facial diagonals, as shown in Figure 4 prepared by A3 student.

Finally, the representation of the plane strictly parallel to one of the faces of the cube that contains another face was correctly performed by almost half of the students (48%) and was the one with the highest number of non-responses (33%). The remaining students (19%) performed such representation in a way that was considered partially correct, as exemplified by the resolution of A8 student, presented in Figure 5. The student shows that he is aware of the property related to the definition of a plane by two parallel lines, but he does not follow the convention, and he does not represent the plane strictly parallel to one of the faces of the cube that contains another face in the form of a parallelogram.

After completing the task with paper and pencil, the students solved the task in pairs using GeoGebra. Analysing the proposed task item by item, only one pair of students (7%) did not represent the cube and only the P11 pair (7%) presented an incorrect answer (Figure 6). In this construction, the edges of the solid do not have the same dimension (2×2×1.5), which reveals the student's lack of critical capacity in identifying the shape represented: a parallelepiped that is not a cube. This is a situation like the one with paper and pencil, where a small number of students did not take into account in their representation one of the cube's properties.

As for the representation of a plane that contains two strictly parallel facial diagonals, six pairs of students (44%) did not answer the question, and two pairs (15%) presented a representation considered incorrect, because the plane represented did not contain the two parallel facial diagonals (Figure 7). Such representation suggests the students represented a plane considering the diagonal of one of the cube faces and a straight line parallel to that diagonal. They guaranteed one of the properties that allowed them to represent a plan, but without responding to the requirements of the question.

Regarding the representation of a plane perpendicular to the plane that contains two strictly parallel facial diagonals that contain two facial diagonals, most students (52%) did not respond. The P7 pair of students (7%) made an incorrect representation when drawing the plane perpendicular to an edge of the cube without guaranteeing that it contained two facial diagonals (Figure 8). From the position of the construction, it is clear that the students had difficulty in mentally 'manipulate' the cube Such a manipulation would have allowed them to confront what they drew with what was asked.

Finally, regarding the representation of a plane strictly parallel to one of the cube faces that contains another cube face, most students (78%) did it correctly while three pairs of students (22%) did not make any sketch.

In summary, the results achieved in the items 'representing a plane containing two strictly parallel facial diagonals of the cube' and 'representing a plane perpendicular to the plane containing two strictly parallel facial diagonals, which contains two facial diagonals' were better with paper and pencil (93% and 48%, respectively) than with GeoGebra (41%). A situation justified by the success of the first approach (with paper and pencil) and which led the students to consider the second approach, with GeoGebra unnecessary. The results in the item 'representing a plane strictly parallel to one of the cube faces that contains another cube face' are better with GeoGebra (70%) than with paper and pencil (48%). This fact indicates differences between the two approaches, suggesting a greater accessibility of the construction in GeoGebra than with paper and pencil. Globally, in paper and pencil approach, the position in which the cube was drawn interfered with the ease or difficulty of representing what was asked. This no longer happens in GeoGebra. In the case of the third question, this is the most difficult to represent with paper and pencil and, therefore, the results are better in GeoGebra.

After completing the task that focused on the 'relative position of lines and planes' in a cube, a prism was explored (Task 2).

An analysis of the students’ answers suggests better results in the approach based in GeoGebra than in the one using paper and pencil (Table 2).

Regarding the representation of a triangular prism with paper and pencil, most students (70%) managed to do it correctly, while A5 student (4%) presented a sketch considered partially correct. The remaining students (26%) did not present any drawing. In the sketch considered partially correct, the student represented the edges of the upper base in a broken line (Figure 9). It is, therefore, a case that does not respect the established conventions for the representation in 2D of 3D figures.

Concerning the representation of a plane perpendicular to the DEF plane, a significant number of students answered correctly (41%) and an equally significant number did not present any sketch (44%). Among the remaining students, three performed a sketch considered partially correct (11%), such as the one made by A11 student (Figure 10), and A1 student (4%) presented a sketch considered incorrect. The sketches where the students did not clearly draw the requested plane were considered partially correct, as shown in Figure 10. In this case the student drew two parallel lines perpendicular to the DEF plane, but he did not use a parallelogram to represent the plane.

In the representation of a plane perpendicular to the DEF plane considered incorrect, A1 student did not label the vertices and drew a single straight line to represent the plane (Figure 11).

In the answers considered correct, the students adequately represented the prism and the plane perpendicular to the DEF plane, as exemplified by the following sketch made by A6 student (Figure 12).

Regarding the resolution of Task 2 using GeoGebra, only one pair of students (7%) did not present any sketch for each situation, with the remaining pairs (93%) making a correct representation, as illustrated by the following construction made by P10 pair of students (Figure 13).

In the constructions that the students carried out, the naming of the vertices did not follow the order shown in the task due to successive attempts to represent the prism. In both items, students revealed a better performance with GeoGebra than with paper and pencil: in the item ‘Represent a triangular prism’ 93% of students did it with GeoGebra while 70% did it with paper and pencil; in the item 'Representing a plane perpendicular to the DEF plane', 93% of the students did it with GeoGebra, as opposed to 41% who did it with paper and pencil.

Conclusion

Almost all students revealed the ability to represent a 3D object, the cube and the prism, using perspective as a technique, based on their orthogonal view, either with paper and pencil or with GeoGebra. The results achieved when representing a cube were better with paper and pencil than with GeoGebra but the results inverted when representing a triangular prism. The greater familiarity with the cube than with the prism (a solid that the students have been working with since the beginning of their geometry schooling), has translated into a greater number of students being able to adequately represent it with paper and pencil. When familiarity with the solid is not as strong, GeoGebra seems to allow for a higher level of success when compared to the paper and pencil approach. In other words, technology seems to facilitate spatial structuring, in the sense presented by Pittalis and Christou (2010), and the consequent representation of the solid in certain phases of the teaching-learning process. The dynamic characteristics of the software GeoGebra seems to be very important here, offering the students’ the opportunity to experiment and explore, which led to a better result at the end.

As for the representation of the plane that contains two facial diagonals, it is more easily done in the cube when it is built with paper and pencil because this is a geometric solid that starts to be analysed very early (as mentioned above), due to the great predominance of it in daily life. This allows for an identification and a deepening of knowledge about its properties and what remains constant in its construction. This prior learning now facilitates working with this solid and its representation.

The properties of a prism can vary depending on the figure that constitutes its base, so its construction with paper and pencil was made with more difficulty by the students. In the case of the representation of a triangular prism and of a plane, the flexibility of GeoGebra favors the representation, which explains the greater efficiency of its representation with this resource.

These results are aligned with the results of previous studies, suggesting within the scope of the representation of 3D objects and their spatial structuring, perceptual abstraction emerges in the identification of basic properties of solids and the internalisation that translates into the respective representations based on such properties, which leads to visualisation in all its senses (Battista, 2007). Conceptualisation results from the recognition of the 3D shape of objects and their properties (Pittalis & Christou, 2010). However, the present study provides evidence about the role played by the resources used, suggesting the potential of digital technologies in the cases where the familiarity with the geometric solid is still under development.

In Task 1, representing a plane parallel to a face that contains another face of the cube implies keeping in mind the concept of parallelism, the concept of plane, the cube properties and relating these concepts to the faces of the solid and also mastering the representation technique for 3D objects. In Task 2, representing a plane perpendicular to a base implies recognising the properties of the triangular prism and those of the plane perpendicular to the DEF base, and relating these concepts. This was easier to achieve when using the GeoGebra, allowing visualisation to acquired greater expression than when performed with paper and pencil. According to the theory of abstraction, interiorisation predominates in this type of geometric reasoning (conceptualisation), since abstraction decouples the object from its original concept, allowing it to be operated on, imagined, and projected onto another object or in another new situation (Battista, 2007).

Generally, it appears that students are more familiar with the cube than with the prism. This familiarity stems from previous experiences, where paper and pencil was dominant. Thus, the representation of the cube was easier with paper and pencil than with GeoGebra, where students did not have the same level of familiarity. However, when the students did not have the same level of familiarity with the solid, GeoGebra seems to have offered a more favorable medium. The combination of these results leads to the conclusion, as Battista (2007) points out, that the joint exploration of GeoGebra and paper and pencil favors the development of students' spatial capacity in learning geometric topics.

In this study, we seek to draw attention to the approaches to geometry in space using paper and pencil and using technology and seek to identify differences between these two approaches based on our experience with a group of 10th grade students. What factors are relevant in both approaches? The students' experience and prior knowledge with each of the solids seems to be determinant in the paper and pencil approach. It is this knowledge that allows the focus on the essential properties of the solid and it is equally this knowledge that allows the drawing of the 3D objects using a 2D representation. In cases where this prior knowledge is more fragile, as in the case of the prism, technology, and, specifically, GeoGebra, emerges as an enhancer, by allowing a representation with different characteristics. What does one approach facilitate over the other? The representations with paper and pencil and with technology are very different, mobilising different knowledge. The main difference is who does the representation. With technology, it is necessary to identify what one wants to represent, but the representation itself is made by the technology based on the indications given by the student. With paper and pencil, it is necessary to effectively perform the representation, which for some students is not easy. In some cases, the difficulty can be further aggravated by the initial representation of the solid which, due to its position, may not allow an adequate representation (for example, by not allowing the drawing of a parallelogram to represent the desired plane).

The fact that the students worked in pairs had the positive impact of allowing discussion among them but it can also limit the experience of one of the elements of the pair with technology, generating some impact on the dynamics of the pair with possible interference in the results of the study. In these circumstances, it seems relevant to consider deepening the conclusions obtained in this study in future research, paying attention to the contribution of each of the elements of the pair (namely regarding the use of technology) and trying to analyse the existence of possible differences between students, according to a more or less intensive use of technology.

Acknowledgments: This work was partially funded by CIEd – Centro de Investigação em Educação, Instituto de Educação, Universidade do Minho, projects UIDB/01661/2020 and UIDP/01661/2020, through national funds of FCT/MCTES-PT; and by national funds through FCT – Foundation for Science and Technology, I.P., within the scope of the project PTDC/CED-EDG/32422/2017.

References

Arcavi, A. (2003). The role of visual representations in the learning of mathematics. Educational Studies in Mathematics, 52, 215-241.

Battista, M. T. (2007). The development of geometric and spatial thinking. In F. K. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 843-907). Information Age Publishing.

Duval, R. (1998). Geometry from a cognitive point of view. In C. Mammana & V. Villani (Eds.), Perspectives on the teaching of geometry for the 21st century (pp. 37-52). Kluwer.

Faggiano, E., Montone, A., & Mariotti, M. (2018). Synergy between manipulative and digital artefacts: A teaching experiment on axial symmetry at primary school. International Journal of Mathematical Education in Science and Technology, 49(8), 1165-1180.

Gagatsis, A., & Geitona, Z. (2021). A multidimensional approach to students’ creativity in geometry: Spatial ability, geometrical figure apprehension and multiple solutions in geometrical problems. Mediterranean Journal for Research in Mathematics Education, 18, 5-16.

Hansen, V. L., Malkevitch, J., & Douady, A. (1998). Geometry: Past and future. In C. Mammana & V. Villani (Eds.), Perspectives on the teaching of geometry for the 21st century (vol. 5, pp. 9-28). Springer.

Jones, K. (2000). Teacher knowledge and professional development in geometry. University of Southampton.

Kokol-Voljc, V. (2007). Use of mathematical software in pre-service teacher training: The case of GeoGebra. In D. Küchemann (Ed.), Proceedings of the British Society for Research into Learning Mathematics, 27(3), 55-60.

Komatsu, K., & Jones, K. (2020). Interplay between paper-and-pencil activity and dynamic-geometry-environment use during generalization and proving. Digital Experiences in Mathematics Education, 6, 123-143.

Koyuncu, I., Akyuz, D., & Cakiroglu, E. (2015). Investigating plane geometry problem-solving strategies of prospective mathematics teachers in technology and paper-and-pencil environments. International Journal of Science and Mathematics Education, 13(4), 837-862.

Lohman, D. (1988). Spatial abilities as traits, processes and knowledge. In R. J. Sternberg (Ed.), Advances in the psychology of human intelligence (Vol. 4, pp. 181-248). LEA.

Maschietto, M., & Soury-Lavergne, S. (2017). The duo “pascaline and e-pascaline”: An example of using material and digital artefacts at primary school. In E. Faggiano, F. Ferrara, & A. Montone (Eds.), Innovation and technology enhancing mathematics education: Perspectives in the digital era (pp. 137-160). Springer.

Osório, V. L., Pino-Fan, L. R., & González, N. (2017). Esquemas argumentativos de estudiantes de secundaria en ambientes de geometría dinámica [Secondary students' argumentative schemes in dynamic geometry environments]. Avances de Investigación en Educación Matemática, 12, 39-57.

Pittalis, M., & Christou, C. (2010). Types of reasoning in 3D geometry thinking and their relation with spatial ability. Educational Studies in Mathematics, 75, 191-212.

Royal Society/Joint Mathematical Council (2001). Teaching and Learning Geometry pre-19. Royal Society/Joint Mathematical Council.

Septia, T., Prahmana, R.C.I., Pebrianto, & Wahyu, R. (2018). Improving students spatial reasoning with course lab. Journal on Mathematics Education, 9(2), 327-336.

Sutiarso, S., Coesamin, M., & Nurhanurawati (2018). The effect of various media scaffolding on increasing understanding of students’ geometry concepts. Journal on Mathematics Education, 9(1), 95-102.

Voltolini, A. (2018). Duo of digital and material artefacts dedicated to the learning of geometry at primary school. In L. Ball, P. Drijvers, S. Ladel, H. Siller, M. Tabach, & C. Vale (Eds.), Uses of technology in primary and secondary mathematics education: Tools, topics and trends (pp. 83-99). Springer.

Floriano Viseu is an assistant professor at Instituto de Educação – Universidade do Minho (Portugal) and a member of the research center CIEd, being coordinator of the Master's degree in Mathematics Education. He holds a Master‘s and a PhD degree in Education, specializing in Didactics of Mathematics. His research interests are centered in mathematics teachers’ knowledge, education of pre-service teachers, and the technology in teaching and learning activities. Email: fviseu@ie.uminho.pt

Helena Rocha is an assistant professor at Faculdade de Ciências e Tecnologia – Universidade NOVA de Lisboa (Portugal) and a member of the research center CICS.NOVA, being coordinator of the Master's degree in Mathematics Education. She holds a Master’s and a PhD degree in Education, specializing in Didactics of Mathematics, and her research interests are centered in mathematics teachers’ knowledge to integrate technology and their professional development. Email: hcr@fct.unl.pt

José Manuel Monteiro is a mathematics school teacher at Escola Secundária Carlos Amarante (Portugal). He has a Master’s in Civil Engineering and another in Mathematics Education. As a school teacher, he is interested in promoting his students’ learning and assumes technology as a possible way of doing that. Email: jmacedomonteiro@gmail.com

Cite this paper as: Viseu, F., Rocha, H., & Monteiro, J. M. (2022). Rethinking digital technology versus paper and pencil in 3D geometry. Journal of Learning for Development, 9(2), 267-278.

Rethinking Digital Technology versus Paper and Pencil in 3D Geometry

Introduction

Methods

Result and Discussion

Conclusion

References