2021 VOL. 8, No. 1
Abstract: This paper reports on a review of a series of video tutorials that were developed for offering at a distance to primary school students of Trinidad and Tobago during the pandemic. The materials selected for the review focused on the teaching of problem-solving skills based on topics drawn from the mathematics curriculum. The tutorials were developed and presented by primary school teachers with support from the Ministry of Education. The main purpose of this review was to assess the instructional strategies employed in the delivery of the video tutorials. An inductive-deductive approach was employed for this purpose. The review also sought to examine the effectiveness of video broadcast to support instructional delivery. The reviewer’s overall conclusion was that greater attention should be paid to formulating strategies specifically for the task of solving a given class of problems, rather than simply relying on the procedures derived from the underpinning mathematical operations. The reviewer made some brief recommendations about the development of a technology-use policy intended to deploy educationally-appropriate modern technology to support the learning of primary school students.
Keywords: primary mathematics, problem-solving teaching strategies, instructional evaluation, technology for learning.
Beyond the statistics about increases in the number of positive COVID-19 cases and deaths, global attention has focused on the disruption that the pandemic has caused in the lives and livelihoods of populations worldwide. In that latter context, education stands out as one of the sectors most seriously affected. In the words of the Secretary-General of the United Nations, “the COVID-19 pandemic has created the largest disruption of education systems in history … affecting nearly 1.6 billion learners in more than 190 countries and all continents.” (UN Policy Brief, August 2020, p. 2). While the immediate effect of the disruption was the rapid adjustments made to continue teaching and learning by distance methods, it also gave administrators and practitioners the opportunity to examine prevailing practices with a view to making overall long-term improvements.
In this context, this paper seeks to examine practices in the area of curriculum delivery in primary education as observed in material made available publicly for students forced to continue their schooling at home.
In April, 2020, the Ministry of Education (MOE) of the Government of the Republic of Trinidad and Tobago (GORTT) launched its online learning platform, named the School Learning Management System (SLMS), to provide students and teachers at the Early Childhood, Primary and Secondary levels with the means to continue teaching and learning remotely. (https://learn.moe.gov.tt) (Loop News, April 14, 2020). According to information provided by the Ministry, about 50 teachers had volunteered to prepare and submit the learning resources that were made available on the SLMS. In addition, teachers, identified by school principals, served as presenters of videotaped lessons for broadcast. The Ministry provided detailed guidelines on how to gain access to the online platform. Parents were also invited to log in, given that, in many cases, they would be required to monitor their children’s online learning activities. (Loop News, March 17, 2020; April 26, 2020)
In the section of the SLMS devoted to primary students, which is the area of interest of this paper, there were sub-sections providing materials for each grade level beginning with Infants (aged 5-6 years) and ending at Standard 5 (aged 11+). Standard 5 is the final grade level in the Primary sector. Students of this class sit the Secondary Entrance Assessment (SEA), which is the examination that facilitates placement in secondary schools.
Alongside the grade level materials, there was a special sub-section focusing specifically on the SEA, given the fact that students were missing out on critical classroom preparation for the examination. This section comprised two components: one, a collection of past examination papers and two, a series of video-recorded tutorials, presented by selected teachers from the school system, and based on topics drawn from the curriculum on which the examination was developed. Each tutorial provided instruction on a topic taken from the curriculum of each of the three subjects assessed in the examination, namely Creative Writing, English Language and Mathematics.
In addition to being uploaded on the SLMS, the SEA video tutorials were broadcast on the state-owned television station, TTT, which, for its part, also made them available on its Facebook page, TTT Live Online. The materials were, therefore, more readily available through this route than via the SLMS and this author opted to take advantage of this additional access route.
For the purposes of this paper, special attention is paid to the SEA subsection and specifically to the video tutorials on Mathematics. The reasons for this decision will be addressed more fully later.
While students, teachers and parents constituted the primary target audience, members of the wider population, including this author, also saw themselves as having a vested interest in this novel undertaking and reserved the right to make comments about it not only privately but through various public fora (e.g., Trinidad and Tobago Guardian, May 2, 2020; Kuboni, Facebook Post, May 5, 2020). The Ministry was therefore under intense scrutiny. Consequently, a considerable amount of information about the roll out of the SLMS was made available through the mainstream media and a lot of it was directed to keeping the population as a whole up-to-date and, hopefully, supportive of the Ministry’s efforts. (CNC3 Editor, April 25, 2020).
Notwithstanding the obvious focus on the immediate goals of the SLMS, this author felt that the pandemic also presented an opportunity to examine prevailing practices in order to make improvements beyond the current emergency situation.
This perspective finds support in the recommendations made in the UN Policy Brief: Education during COVID-19 and beyond. One of the recommendations of this document calls for policymakers to “reimagine education and accelerate positive change in teaching and learning”. Expanding on that idea, it further states, “As we ‘build back resilient’, we need to ensure that education systems are more flexible, equitable, and inclusive (UN Policy Brief, August 2020, p. 23).
The concern for greater equity and inclusion in the education system has particular relevance for primary and secondary education in Trinidad and Tobago, with the SEA occupying a very pivotal position across both sectors. This examination is critical in the life of every child 11 years and over as it is the vehicle that facilitates their transition from primary to secondary school. Approximately 18,000 students take the exam every year. While there are enough places in the secondary sector to accommodate almost all the children sitting the exam, only a small proportion of them will enter schools that are deemed to be of a high quality. It is beyond the scope and purpose of this paper to examine the SEA or even to explore the factors contributing to this disparity among secondary (and even primary) schools in the system. The only point of relevance in this context is that students with the highest scores in the examination are placed in the so-called ‘prestige’ secondary schools and those with the lowest scores are placed in schools that are deemed to be of a lower rank.
What this situation brings into focus, is the generally held view that there is a relationship between academic achievement and socio-economic status and that low socio-economic status typically correlates with low academic achievement (Devlin, 2013, Rigaud, 2013, Yelgun & Karaman, 2015). It is reasonable to infer therefore that those who were most deprived in the pre-COVID era would be the ones most challenged in these circumstances, and that the gap between high and low achievers in the primary school sector would widen even further. The study was therefore undertaken to review materials that were developed to provide instruction, at a distance, for all Standard 5 students due to sit the SEA in the current year.
Mathematics has been singled out as an area of low achievement in the primary school system of Trinidad and Tobago (Alexander & Maeda, 2015; Khan, 2017). For this reason, the author identified the Mathematics materials for special study.
The Mathematics component of the exam is based on four subject-matter strands, namely, Number, Measurement, Geometry and Statistics and entails the assessment of three types of thinking processes, namely, knowing, applying and reasoning in each strand. A closer look at the objectives associated with each of the thinking processes reveals that the task of problem solving is included, to some extent, in the process of applying, and definitely in relation to reasoning. Examples are as follows:
Strand |
Sub-section of Strand |
Process |
Objective |
Numbers |
Whole numbers |
Applying |
Solve one-step word problems involving any one of the four basic operations on whole numbers. |
|
|
Reasoning |
Solve multi-step word problems involving any combination of the four basic operations on whole numbers. |
|
Fractions |
Reasoning |
Solve multi-step problems involving fractions. |
|
Percent |
Reasoning |
Solve problems involving unequal sharing. |
Measurement |
Area and perimeter |
Reasoning |
Solve problems involving area and perimeter of plane shapes. |
|
|
|
Solve problems in real-life contexts involving area. |
|
Time |
Reasoning |
Solve computational and real-life problems involving hours and minutes. |
Geometry |
Symmetry |
Reasoning |
Solve problems involving line symmetry. |
Statistics |
|
Reasoning |
Use analysed data to solve problems, draw conclusions and make decisions. |
|
|
Reasoning |
Solve problems involving mean/average. |
(https://www.moe.gov.tt/sea-2019-2023-framework/)
Almost all the video tutorials were based on problem-solving tasks using content derived from one or other of the strands identified.
In this regard, the SEA Mathematics materials, and by extension the curriculum guides from which they were derived, are consistent with the practice in other jurisdictions that place a high priority on problem-solving skills in the primary school Mathematics curriculum. This author regards the explanation provided by Phonapichatt, Wongwanich & Sujiva (2014) to be a useful starting point for understanding the nature of the activity. They assert:
A mathematical problem in this study means a mathematics-related question or situation that highly varies. It is a real situation seen in real life which requires a proper method and mathematical knowledge in order to be solved. (p. 3171).
It is against the background of the details outlined above that this author embarked on a study to assess the problem-solving strategies employed by the instructors in the video tutorials. Five video tutorials, on the topics ‘Simple Interest’, ‘Perimeter and Area’, ‘Percent’, ‘Division with Fractions’ and ‘Unequal Shares’ were reviewed. These were accessed from the ‘S.E.A Time’ segment of the Facebook Page TTT Live Online during the period July to mid-August, 2020.
(https://www.facebook.com/watch/tttliveonline/)
While the assessment focuses mainly on the problem-solving strategies that the video tutors utilised, attention is also paid to the broadcast medium used to deliver the instruction.
The study seeks to assess the instructional strategies employed in the delivery of the video tutorials to facilitate the development of mathematical problem-solving skills in students preparing for the SEA.
The study also seeks to examine the effectiveness of the video broadcasts to support instructional delivery.
Finally, the study makes recommendations for rethinking this aspect of the mathematics curriculum and for formulating a policy for technology-enhanced curriculum delivery in the primary education sector of Trinidad and Tobago, to support learning both during and beyond the period of the pandemic.
An inductive-deductive approach (Burney & Saleem, 2008; Soiferman, 2010) was used to conduct this study. In the first stage, the reviewer went through each of the selected tutorials at least twice taking note of areas of interest from an instructional perspective and observing similarities and differences between and among teaching methods employed in the respective tutorials. Thereafter, based on further study of these specific methods, the reviewer categorized them into broader instructional strategies.
Ultimately, the strategies emerging from this study were used to do a closer, more in-depth assessment of the tutorials.
The five Mathematics video tutorials that were downloaded were added to the author’s set of saved items on her Facebook page and included in a special collection labelled, ‘COVID and Schooling’.
As noted earlier, the reviewer browsed through each of the five videos, paying special attention to the methods used for instructional delivery, and thereafter categorizing these into broader instructional strategies. In order to ascertain whether the strategies identified in this study were consistent with those that feature in the wider field of study into mathematical problem-solving strategies, the reviewer conducted a brief examination of the relevant literature.
Each instructional strategy was then used to conduct a more in-depth analysis of the tutorials. The elements of the tutorial analysed were the oral presentation of the tutor, accompanying information provided on the whiteboard, and demonstrations using teaching aids. The most appropriate tutorial was selected for the analysis of a given instructional strategy.
The study focuses exclusively on the instructional strategies employed by the tutors in the delivery of the video tutorials. It does not seek to examine learning outcomes. Neither is it intended as an evaluation of individual video tutorials. Rather, it seeks to analyse some instructional strategies used within the tutorials with a view to highlighting their strengths and/or weaknesses in relation to the overall goal of facilitating the development of problem-solving skills. Where appropriate, it offers suggestions for improvement.
Two limitations are to be noted. First, the video tutorials chosen for download were arbitrarily selected. No systematic procedure was employed. Nonetheless, in the opinion of the author, the five selected represented a good cross-section of the available pool.
Secondly, the findings obtained by the author/reviewer were not validated by a second reviewer. While this key requirement cannot be downplayed, there are two other aspects of the study that, in some way, can partially compensate for its absence. The author is of the view that the decision to identify similar strategies in the broader literature can serve to show some consistency with similar work in the field. In addition, the author believes that her own experience as a teacher, teacher educator and educational technologist has equipped her with the tools to conduct a reasonable assessment of the materials.
The benefits of using this delivery mode are applicable both in terms of its reach as well as the standard of production that it makes possible.
Since a large number of students were unable to access the SLMS, delivering content in this mode and making it available via television, was a major advantage. Moreover, Trinidad and Tobago Television (TTT), the state-owned television network of Trinidad and Tobago, enjoys good reception across both islands, including in rural areas.
All the tutorials were carefully prepared. Most were divided into segments, with each successive segment building on the one preceding it. What this ensured was that the same standard of materials was available for all viewers.
The production of the tutorials benefitted immensely from the professional input of the production staff of TTT. Of special significance was the variation in camera angles employed. Close-ups were used to good effect to allow students to zero in on some detail or some written material on the whiteboard, or some activity that the tutor was engaged in. Wide angled shots allowed viewers to see all aspects of the teaching space in relation to one another.
Another feature to be noted was the simulated interactive style that the tutors adopted in delivering their presentations. They demonstrated that they were very aware of the need to enhance their delivery in order to connect with their distant viewing audience. Judging from posts in the ‘Chat’ linked to the Face Book presentations, some presenters were able to stimulate their viewers to respond and even initiate discussion points during their presentations. While these viewers may not necessarily have been students, the fact that the presentations were able to elicit these responses should be noted.
Notwithstanding these positive features of the broadcast mode, there were some limitations that should not be ignored. Basically, delivery of this type mimics the one-to-many lecture style of the ‘live’ classroom. Even though, in both cases, there are strategies to foster two-way communication, this is limited. In fact, in reality, there is no two-way communication when the material is pre-recorded.
Another limitation is that the format, as a stand-alone vehicle, is incapable of adequately handling all facets of the instructional delivery required. Notwithstanding the best efforts of the tutors, it was evident that some aspects of the content may not have been treated to the extent required. The point being made here is that while stand-alone video broadcasting, transmitted by television to a mass audience, can serve important school-related purposes in emergency situations, there are limitations that should also be acknowledged.
Five strategies emerged from the preliminary analysis and were used to facilitate closer examination of the approach to instructional delivery. Moreover, as stated earlier, efforts were made to ascertain the extent to which these strategies were reflective of the wider pool used to facilitate the development of problem-solving skills.
Clarifying Key Concepts
At the beginning of a tutorial, the tutor would identify and define the key concepts embedded in the problem-solving activity to be taught. In almost all instances, she would also remind the distance students about the importance of remembering the explanation as they embarked on the activity. The role of concept definition is examined in relation to two tutorial topics.
The two terms in the topic ‘Perimeter and Area’, were identified as the concepts to be explained.
(https://www.facebook.com/watch/?ref=saved&v=300611234289110)
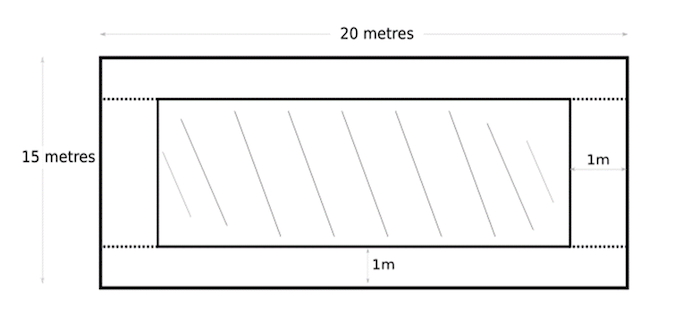
Perimeter was described as “distance around a shape or an object” and Area, as “surface covered”. Applying the meaning of these two concepts to the shapes of a square and a rectangle, the tutor was able to generate formulae for calculating both the perimeter and the area, which could then be applied for problem solving. Following are two of the problems worked on:
What we have in both problems is a direct connection between what students were expected to know about the two key concepts and what the respective problems required them to do. However, when we examine a third problem based on this same topic, the connection is not so readily recognisable. That problem reads:
A few questions arise here. Is this problem dealing with “surface covered” or “distance around”? Is the student required to calculate area or perimeter? An important difference between this problem and the first two, is that this one does not clearly show a link to the two key concepts and this may turn out to be a stumbling block for many students.
For the topic ‘Simple Interest’, four concepts were identified, namely Simple Interest, Principal, Rate, and Time.
(https://www.facebook.com/watch/?ref=saved&v=323968835647872)
All four combine to yield the formula:
Prior to generating this formula, the tutor provided explanations for each of the four concepts. The first two were defined as follows:
The definition of these two concepts is based on the assumption that students already have a clear understanding of the subsidiary terms, ‘fee’, ‘loan’, ‘borrow’ and ‘invest’. In addition, the tutor is also assuming that students would not conflate this new term ‘Principal’ with the title used for the person who is the head of the school! Ultimately, some students may resort to rote memorization, which is likely to impede understanding even further.
In seeking to clarify key concepts, teachers may wish to consider expanding on the bare essential explanation in order to give students the best possible chance of grasping all relevant dimensions of the new term.
This perspective seems to find support in a study conducted among elementary Puerto Rican students. Based on an investigation of students’ ability to understand word problems involving ratio, that researcher concluded that the study provided “evidence that the meaning of concepts and relationships in a two-step word problem is a major source of difficulty in solving the problem”. (Quintero, 1983, p. 111)
Dissecting the Text
The issue regarding the understanding of concepts is part of a wider concern about capacity to unpack the language through which the problem is conveyed. Often, the typical expressions associated with mathematical operations are not always used in constructing the problem statement. As a result, students must rely on prior language competence to locate core mathematics-related information.
The following problem taken from the tutorial ‘Division with Fractions’, poses such a challenge:
(https://www.facebook.com/watch/?ref=saved&v=3242415585801979)
Looking only at the first part of the problem, there is nothing that overtly indicates that it entails division by fractions. With careful reading, some students may be able to come to that conclusion, but others may not. Including the second part was very likely intended to ensure that all students have the same basic information to undertake the task.
Students’ ability to dissect the text of a problem in order to extract the core information needed to initiate the problem-solving task is an area that requires its own focussed attention. Of relevance in this regard is the conclusion arrived at in a 2008 study that “children’s text comprehension skills and mathematical word problem-solving performance were interrelated.” (Vilenius-Tuohimaa, Aunola, & Nurmi, 2008, p. 422).
From the Concrete to the Abstract
The use of manipulatives to facilitate learning transfer from the concrete to the abstract is well-documented (e.g., Kamina & Iyer, 2009). Manipulatives featured in several tutorials to introduce students to mathematical operations at the level of the concrete and which they could eventually encounter in a more abstract form. These operations could, in turn, be applied in order to arrive at a solution for relevant word problems. Based on observations made of tutors’ handling of the teaching aids, two recommendations are pertinent here. First, teachers must ensure that the objective(s) adopted for conducting the demonstration with the teaching aids are consistent with those of the related abstract operations and, by extension, with the class of problems to be solved. Secondly, teachers must have a plan to take the students to a point where they (the students) can confidently make the transition from concrete operations to the realm of abstract thinking, not only in terms of doing abstract calculations but also in terms of applying those operations in order to generate solutions to the relevant problems.
One tutorial in which extensive use was made of teaching aids was the one on Percent (Percentage). Cuisenaire rods, flats, and a fraction board were the objects used to initiate the instruction.
(https://www.facebook.com/watch/?ref=saved&v=1283760121827062)
Based on the tutorial objectives, students were expected to:
However, immediately after these objectives were stated, the tutorial shifted focus to a problem involving fractions, which stated:
For about the first twenty-five minutes of the tutorial, the focus of the activity being carried out with the teaching aids was fractions, and specifically fractions with a denominator of a hundred. The teaching aids were used to demonstrate a part of a whole as a fraction. It was only towards the end of the first half that percent was introduced. A grid, divided into one hundred parts, was introduced at this point and presented decimals and percent as equivalents of the fractions previously generated using the teaching aids. The segment then concluded with a conversion table showing selected fractions and their equivalents as decimals and percent. In the latter part of the tutorial, problems consistent with the original objectives were introduced. However, the content learned using the teaching aids was largely ignored during this segment. Thus, there was no carryover from demonstration to problem-solving activity.
One is not attempting to question the validity of the linear approach to calculating the percent, starting at the level of fractions. Rather, the point being made here is that the objective and strategy that guided the use of the teaching aids were not consistent with the overall objectives of the tutorial.
Using Line Drawings to Model more Complex Phenomena
Line drawings, like the teaching aids discussed above, provide an avenue for students to encounter abstract ideas in a form that is more concrete and, as such, more readily understood. One author uses the expression ‘diagramming the problem’ to refer to this activity (Zambo, 1992, p. 153). However, it should also be noted that line drawings are ‘less concrete’ than the typical teaching aids and function at a higher level of abstraction than the more concrete objects. Two ways in which they were used are noted here.
In one instance, a line drawing was used to provide a simplified representation of a more complex real-world phenomenon, in order to highlight features that students were required to pay attention to. In another instance, simplified line drawings served as an explanatory tool to clarify and make more accessible the core meaning of mathematical expressions. Examples of both are shown below.
With regard to the first, a simple diagram, drawn on the whiteboard in the tutorial on Perimeter and Area, served to illustrate the word problem below it.
(https://www.facebook.com/watch/?ref=saved&v=300611234289110)

Whether consciously acknowledged or not, this problem is making certain assumptions about the students. For example,
Overall, this type of problem is based on the assumption that even before students undertake the required mathematical operations, they must draw on some underlying prior knowledge in order to set the stage for carrying them out.
Line drawings were also used to render abstract operations in a more concrete form and, as a result, more readily understood by students. In the tutorial dealing with the topic ‘Division with Fractions’, line drawings were used extensively to bring greater clarity to operations that, in their abstract form, may not have been readily understood.
(https://www.facebook.com/watch/?ref=saved&v=3242415585801979)
The statement below applies to the set of mathematical operations that follow it. Note the line drawings accompanying each example of a division by a unit fraction.
For each whole divided by a unit fraction, the result is the total number of unit fractions that form the whole.
1 ÷ ½ = 2
| 1 | 2 |
1 ÷ ¼ = 4
| 1 | 2 | 3 | 4 |
1 ÷ 1/5 = 5
| 1 | 2 | 3 | 4 | 5 |
1 ÷ 1/12 = 12
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
This set of diagrams formed part of an instructional sequence in the first segment of the tutorial, the purpose of which was to reinforce the statement that:
Dividing any number by a unit fraction is the same as multiplying the number by the reciprocal of the unit fraction.
When using line drawings as an explanatory tool, it is important to ensure that each successive drawing (or set of drawings) builds on its predecessor, with appropriate additional information, so as to provide a logical, well-ordered path to the ultimate content to be learned. Reducing and/or removing them prematurely may compromise the student’s ability to reach the intended learning target, as was probably the case in this tutorial.
Formulating a Specific Strategy for Problem Solving
In the final analysis, what students require from the instruction provided by the tutor is a complete well-integrated strategy to guide the problem-solving activity. All the elements must blend together in order to efficiently support them in carrying out the task of generating a solution to the given problem. Such a strategy must meet three essential criteria. First, it must be directly applicable to a particular category of problems. Second, it must be robust enough to hold together over several applications. Third, even as it holds together, it must still be flexible enough so that it may be adapted in instances where a given problem, though belonging to a particular category, varies from the typical.
While it is the tutor (teacher) who initiates the formulation of the strategy, it is the student who eventually must put it to use. Consequently, the student must come to know the strategy and take control of it in order to use it. Two issues are to be noted in this regard.
In some tutorials, the strategy for solving the problem was more clearly articulated than others. Two examples of the former were ‘Perimeter/Area’ and ‘Simple Interest’1. A closer examination of these two revealed that the related problems were closely tied to the mathematical operations on which they were based. Further, for each, actual written formulae were provided as a follow-up to the explanation of the operation. This was even more clearly done in the case of the ‘Perimeter/Area’ tutorial. Thus, even when the problem veered slightly away from the mathematical operation, one could expect that the same strategy, based on the mathematical operation, would provide adequate support for working out the solution.
Two others that did not fit into this mould were ‘Division with Fractions’ and ‘Unequal Shares’. In the case of the former, a substantial portion of the tutorial was dedicated to an explanation of various division by fraction operations, with accompanying formulae to reinforce the calculations. The latter part of the tutorial featured word problems based on the preceding operations. However, the close link detected between mathematical operations and problems in the ‘Perimeter/Area’ and ‘Simple Interest’ tutorials was not always evident in the problems on ‘Division with Fractions’. The following problem brings this issue to the fore:
Even though it is expected that procedures related to the mathematical operation, ‘Division with Fractions’ would play a part in the solution of this problem, there was clearly need for some intermediary guidelines, specific to this category of problems, to link the problem with the procedures related to that mathematical operation. Such guidelines could be expected to assist students in their interpretation of the problem and put them on the path to working out its solution. However, this was not done. What was provided, though, were four broad steps, broken down into sub-steps, that could, in fact, apply to any problem-type. The four were:
It is very unlikely that students, working on their own, would be able to make any meaningful use of these steps.
Unlike ‘Division with Fractions’, the problems on ‘Unequal Sharing’ were not linked to a formal set of mathematical operations. However, similar to the former, there were a set of general steps. These were, “read, plan, do, check”, with additional “things to remember when you read a problem”, namely:
(https://www.facebook.com/tttliveonline/videos/261474185017089)
In delivering the instruction for this latter group of problems, the tutor did, in fact, use strategies that were based on the broad guidelines provided. There was frequent use of diagrams to support her oral explanation of the procedures being applied. Overall, though, the combination of diagrams and explanations did not seem to be grounded in a formalised set of rules that could apply over a whole group of problems. Nonetheless, one got a sense that the tutor was drawing on an internal knowledge base, even though it was not conveyed in a very well organised way.
One should not underestimate the value of clear problem-specific instructions to guide the solution of particular categories of problems. This perspective is being proposed even in instances where the procedures developed for the calculation of the base operations appear to offer good support for the related problem-solving exercise. The question that emerges in such cases is whether the same will hold true when the problems become more complex.
One should not assume that the instruction provided to support the learning of the base operations, would automatically transfer to the task of solving related word problems, even though the transition that the tutor makes may appear to be seamless. For the average student, knowing how to divide by fractions, or even calculating the perimeter and area of plane shapes, may not necessarily provide him or her with all the tools for solving problems based on those operations. The point being emphasized here is that problem-solving tasks require their own procedures in their own right.
A useful starting point for formulating appropriate strategies may lie in the oral communication of teachers themselves. Such communication is drawing on an internal knowledge base that may be more substantial than what is openly shared with the students. Unpacking that spoken text, inclusive of teacher-student interactions (whether simulated or real), while simultaneously tapping into the internal knowledge base, should be a critical part of the exercise of formulating well-constructed strategies that students can take ownership of.
Even as one acknowledges the need for strategy formulation geared to satisfy the requirements of a specific problem type, one needs to be wary of conveying the impression that there is a single strategy that will apply to all possible problems that fall within the same topic area. Consequently, an important aspect of building capacity for problem solving is for teachers to be aware that they are assisting students to build a strategy that can, not only work in its own right, but which they (the students) will be required to adjust from time to time given variations in the problems to be solved. Students’ ability to vary existing strategies to meet the requirements of slightly different problems, or alternatively to generate a new strategy, will be dependent on the extent to which they have a substantial body of already developed strategies that they can draw on to construct something (almost) new.
While this review was conducted on video tutorials developed to facilitate remote teaching during the pandemic, it is the intention of the reviewer that the actual assessment would apply to any teaching mode, whether at a distance or face-to-face. At the same time, given the way the pandemic has thrust matters regarding the role of technology in education to the fore, the reviewer recognises the need to address this issue not only in relation to the teaching of problem-solving skills, but to primary education as a whole.
With regard to problem-solving skills, there was a need for improvement in specific aspects of the instruction, namely:
One acknowledges that not all of the strategies could or should be accommodated under a single umbrella. Consequently, what is also required is a broad-based appraisal of the curriculum both within and across content areas to make the necessary adjustments.
The approach described above is consistent with the fundamentals of Pedagogical Content Knowledge (PCK), described as “the knowledge that teachers develop over time, and through experience, about how to teach particular content in particular ways in order to lead to enhanced student understanding” (Loughran, Berry & Mulhall, 2012, p. 7)
In terms of technology use, given the emergency situation that continues to prevail, the heavy reliance on broadcast (as well as remote teaching via videoconferencing) was necessary. However, notwithstanding the advantages of video broadcast discussed earlier, its limitations cannot be ignored.
This reviewer is of the view that there is a need to develop a technology-use policy for the primary sector (and in fact for the entire education system) that leads it out of the reactive, unsustainable situation it now finds itself in, and which is widening an already big gap between low and high performers. Such a policy would aim to provide all students with access to educationally-appropriate modern technology. For this to happen, there is a need for a shift in thinking away from a laptop for every child, to one that places the emphasis on outfitting all schools with the necessary hardware and software as well as Internet connectivity for communal use. The intention here is to re-establish the school compound as a significant centre of learning in the life of the child, and by extension, to make it the main location for student use of the technologies for purposes of learning.
Some may argue that such a position does not take into account the possibility that the country can be plunged into another phase of increased virus spread. This author would respond with the counter-argument that it is not in the interest of a large proportion of the school population for them to be subjected to ongoing remote lecture-type teaching.
There is a need to re-orient thinking on the relationship between technology and learning. Norton and Wiburg (1998) appear to be addressing that issue when they assert:
When educators design learning opportunities for students, they must choose the tool or combination of tools consistent with the intellectual challenges at hand. (p. 38)
Whether the content to be learnt relates to the solving of word problems in mathematics or any other area of learning, the positions articulated above are provided as a useful starting point for contemplating the design and development of the learning experience.
The issues regarding inadequate clarification of concepts in these two tutorials, that were discussed earlier, have been temporarily set aside for the purpose of the current discussion.
Alexander, V., & Maeda, Y. (2015). Understanding student achievement in mathematics and science: The case of Trinidad and Tobago. Prospects, 45, 577-591.
Burney, S. M. A., & Saleem, H. (2008). Inductive and deductive research approach. Monograph for lecture presentation. University of Karachi, Pakistan.
CNC3 Editor (April 25, 2020). Education Ministry: Online platforms a success. https://www.cnc3.co.tt/education-ministry-online-platforms-a-success/
Devlin, M. (2013). Bridging socio-cultural incongruity: Conceptualising the success of students from low socio-economic status backgrounds in Australian higher education. Studies in Higher Education, 38(6), 939-949.
Kamina, P., & Iyer, N. (2009). From concrete to abstract: Teaching for transfer of learning when using manipulatives. University of Connecticut: NERA Conference Proceedings.
Khan, S. A. (February 8, 2017). Mathematics proficiency of primary school students in Trinidad and Tobago. (Submitted in partial fulfilment of the requirements for the degree of Doctor of Education.) Teachers’ College, Columbia University.
Kuboni, O. (May 5, 2020). Schooling in the time of Covid-19 and beyond in T&T. https://www.facebook.com/notes/olabisi-kuboni/schooling-in-the-time-of-covid-19-and-beyond-in-tt/2944993535590453
Loop News (March 17, 2020). COVID-19: MOE seeks teachers to volunteer, submit content. http://www.looptt.com/content/covid-19-moe-seeks-teachers-volunteer-sumbit-content
Loop News (April 14, 2020). How to access the Education Ministry’s online learning platform. http://www.looptt.com/content/how-access-education-ministrys-online-learning-platform
Loop News (April 26, 2020). Ministry arranging internet access, devices for vulnerable students. http://www.looptt.com/content/ministry-arranging-internet-access-devices-vulnerable-students
Loughran, J., Berry A., & Mulhall, P. (2012). Pedagogical content knowledge. In J. Loughran, A. Berry & P. Mulhall (Eds.), Understanding and developing science teachers’ pedagogical content knowledge, 7-14.
Norton, P., & Wiburg, K. (1998). Teaching with technology. Harcourt Brace College Publishers.
Phonapichatt, P., Wongwanich, S., & Sujiva, S. (2014). An analysis of elementary school students’ difficulties in mathematical problem solving. Procedia – Social and Behavioral Sciences, 116, 3169-3174.
Quintero, A. H. (1983). Conceptual understanding in solving two-step word problems with a ratio. Journal for Research in Mathematics Education, 14(2), 102-112.
Rigaud, P. (2013). Investigating school performance in the primary sector of Trinidad and Tobago: An embedded case study. Biennial conference of the University of the West Indies School of Education, St. Augustine Campus.
Soiferman, L. K. (2010). Compare and contrast inductive and deductive research approaches. University of Manitoba.
Trinidad and Tobago Guardian (May 2, 2020). 60,000 students suffering. https://www.guardian.co.tt/news/60000-students-suffering-6.2.1109261.6ee28d9d13
TTT Live Online (2021). S.E.A. Time. https://www.facebook.com/watch/tttliveonline/
United Nations (2020, August). Policy brief: Education during COVID-19 and beyond. https://www.un.org/sites/un2.un.org/files/sg_policy_brief_covid-19_and_education_august_2020.pdf
Vilenius-Tuohimaa, P., Aunola, K., & Nurmi, J. (2008). The association between mathematical word problems and reading comprehension. Educational Psychology, 28(4), 409-426.
Yelgun, A., & Karaman, I. (2015). What are the factors reducing the academic achievement in a primary school located in a neighbourhood with a low socio-economic status? Education and Science, 40(178), 251-268.
Zambo, R. (1992). Word problem solving in middle grades mathematics. Research in Middle Level Education, 16(1), 143-157.
Author:
Dr Olabisi Kuboni is an Independent Consultant in open and distributed learning based in Trinidad and Tobago. She retired as Senior Lecturer and Head of Graduate Programmes at the University of West Indies Open Campus in 2012. Her research and development interests include support systems for the online learner, the analysis of online teaching-learning strategies and the design and development of management systems to support online learning. Dr Kuboni was a recipient of the COL Fellow Award in 2013. Email: olabisikuboni99@gmail.com
Cite this paper as: Kuboni, O. (2021). Rethinking problem-solving teaching strategies in the primary sector for both face-to-face and online delivery. Journal of Learning for Development, 8(1), 42-57.